题目内容
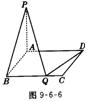
(12分)(理)如图9-6-6,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(1)问BC边上是否存在Q点,使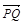 ⊥
⊥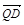 ,说明理由.
,说明理由.
(2)问当Q点惟一,且cos<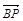 ,
,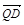 >=
>=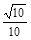 时,求点P的位置.
时,求点P的位置.
【答案】
解:(1)如答图9-6-2所示,建立空间直角坐标系A一xyz,设P(0,0,z),
D(0,a,0),Q(1,y,0),
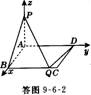
则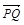 =(1,y,-z),
=(1,y,-z),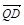 =(-1,a-y,0),且
=(-1,a-y,0),且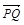 ⊥
⊥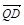 .
.
∴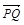 ·
·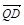 -1+y(a-y)=0
-1+y(a-y)=0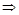 y2-ay+1=0.
y2-ay+1=0.
∴△=a2-4.
当a>2时,△>0,存在两个符合条件的Q点;
当a=2时,△=0,存在惟一一个符合条件的Q点;
当a<2时,△<0,不存在符合条件的Q点.
(2)当Q点惟一时,由5题知,a=2,y=1.
∴B(1,0,0),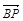 =(-1,0,z),
=(-1,0,z),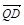 =(-1,1,0).
=(-1,1,0).
∴cos<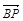 ,
,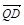 >=
>=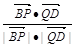 =
=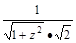 =
=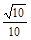 .
.
∴z=2.即P在距A点2个单位处.
【解析】略

练习册系列答案
相关题目