题目内容
(文)设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的.现投掷骰子根据其点数决定棋子是否移动;若掷出的点数是奇数,则棋子不动;若掷出的点数是偶数,棋子移动到另一顶点,若棋子的初始位置在顶点A,回答下列问题:
(1)投了2次骰子,棋子才到达顶点B的概率是多少?
(2)投了3次骰子,棋子恰巧在顶点B的概率是多少?
解:(1)“投了2次骰子,棋子才到达顶点B”包含两种情况:
“第一次不动,第二次移到点B”、“第一次移到C或D,第二次移到B”;
所求概率为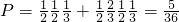 …(6分)
…(6分)
(2)“投掷3次骰子,棋子恰巧在顶点B”包含三种情况:
“三次中棋子恰移动一次”、“三次中棋子恰移动两次”、“三次中棋子恰移动三次”
所求概率为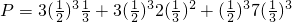 =
=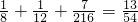 …(12分)
…(12分)
分析:(1)本题研究事件“投了2次骰子,棋子才到达顶点B”的概率,此事件包含两种情况“第一次不动,第二次移到点B”、“第一次移到C或D,第二次移到B”分别计算出它们的概率,再求和既得;
(2)本题研究的事件“投掷3次骰子,棋子恰巧在顶点B”包含三种情况:“三次中棋子恰移动一次”、“三次中棋子恰移动两次”、“三次中棋子恰移动三次”,分别求出每一种情况下的概率,再求它们的和.
点评:本题考查相互独立事件的概率乘法公式,事件的分类,解题的关键是理解所研究的事件包含了哪些事件,且能根据概率乘法公式正确进行计算求概率,本题的难点是理解事件,对事件所包含的情况进行分类,重点是从事件中抽象出概率乘法模型,利用公式进行计算.本题考查了分类讨论思想,转化的思想及从具体事件中抽象出概率模型的能力,这也是高考考查的主要方式
“第一次不动,第二次移到点B”、“第一次移到C或D,第二次移到B”;
所求概率为
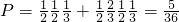 …(6分)
…(6分)(2)“投掷3次骰子,棋子恰巧在顶点B”包含三种情况:
“三次中棋子恰移动一次”、“三次中棋子恰移动两次”、“三次中棋子恰移动三次”
所求概率为
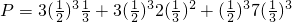 =
=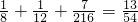 …(12分)
…(12分)分析:(1)本题研究事件“投了2次骰子,棋子才到达顶点B”的概率,此事件包含两种情况“第一次不动,第二次移到点B”、“第一次移到C或D,第二次移到B”分别计算出它们的概率,再求和既得;
(2)本题研究的事件“投掷3次骰子,棋子恰巧在顶点B”包含三种情况:“三次中棋子恰移动一次”、“三次中棋子恰移动两次”、“三次中棋子恰移动三次”,分别求出每一种情况下的概率,再求它们的和.
点评:本题考查相互独立事件的概率乘法公式,事件的分类,解题的关键是理解所研究的事件包含了哪些事件,且能根据概率乘法公式正确进行计算求概率,本题的难点是理解事件,对事件所包含的情况进行分类,重点是从事件中抽象出概率乘法模型,利用公式进行计算.本题考查了分类讨论思想,转化的思想及从具体事件中抽象出概率模型的能力,这也是高考考查的主要方式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目