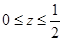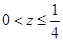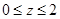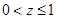题目内容
已知 ,求
,求 的最大值。
的最大值。
 ,求
,求 的最大值。
的最大值。
【错解分析】

 ,即
,即 的最大值为
的最大值为 。
。【正解】解法一:
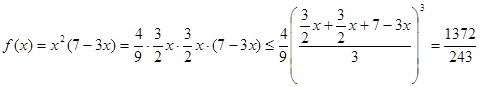
因此,当且仅当
 时,
时, 的最大值为
的最大值为 。
。解法二:(用导数知识解)

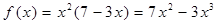 ,
,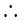
 ,令
,令 ,得
,得 或
或
又
 ,且当
,且当 时,
时, ;当
;当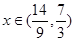 时,
时,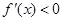
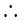 当
当 时,
时, 的最大值为
的最大值为 。
。【点评】在应用均值不等式解题时,要注意它的三个前提条件缺一不可即“一正、二定、三相等”,错解中忽视了均值不等式中等号成立的第三个条件,因为无论
 在
在 中取何值,等式
中取何值,等式 都不成立。
都不成立。
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 若
若 的最大值为8,则k=_____
的最大值为8,则k=_____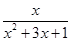 ≤a恒成立,则a的取值范围是________.
≤a恒成立,则a的取值范围是________. 在由不等式组
在由不等式组 确定的平面区域内,则点
确定的平面区域内,则点 所在平面区域的面积是 。
所在平面区域的面积是 。


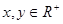 ,且2x+8y-xy=0则x+y的范围是 。
,且2x+8y-xy=0则x+y的范围是 。 ,若
,若 ,
, ,则
,则 的最大值为( )
的最大值为( )

 恒成立,则m的最大值是
恒成立,则m的最大值是 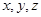 满足
满足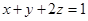 ,
,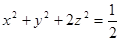 ,则
,则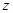 的取值范围是( )
的取值范围是( )