题目内容
已知椭圆C的两焦点为F1(-1,0),F2(1,0),并且经过点M(1 ,| 3 | 2 |
(1)求椭圆C的方程;
(2)已知圆O:x2+y2=1,直线l:mx+ny=1,证明当点P(m,n)在椭圆C上运动时,直线l与圆O恒相交;并求直线l被圆O所截得的弦长的取值范围.
分析:(1)解法一由椭圆的定义知2a=|MF1|+|MF2|=4,得到a=2,又c=1根据a,b,c的关系b2=a2-c2=3故得到a=2,b=
,进而可得答案;
解法二利用待定系数法设椭圆方程为
+
=1,将M点的坐标代入得
+
=1又a2=b2+1所以可得a2=4,b2=3,进而可得答案;
(2)点P在椭圆上即
+
=1所以m2+n2>
+
=1,所以圆心到直线的距离小于半径r,所以直线l与圆O相交.所以弦长l=L=2
=2
又0≤m2≤4所以
≤L≤
.
| 3 |
解法二利用待定系数法设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 12 |
| a2 |
(
| ||
| b2 |
(2)点P在椭圆上即
| m2 |
| 4 |
| n2 |
| 3 |
| m2 |
| 4 |
| n2 |
| 3 |
| 1-d2 |
1-
|
2
| ||
| 3 |
| 3 |
解答:解:(1)解法一:设椭圆C的标准方程为
+
=1(a>b>0),
由椭圆的定义知:2a=
+
=4 , c=1 , b2=a2-c2=3
得a=2,b=
故C的方程为
+
=1.
解法二:设椭圆C的标准方程为
+
=1(a>b>0),
依题意,a2=b2+1①,将点M(1,
)坐标代入得
+
=1②
由①②解得a2=4,b2=3,故C的方程为
+
=1.
(2)因为点P(m,n)在椭圆C上运动,所以
+
=1,则m2+n2>
+
=1,
从而圆心O到直线l:mx+ny=1的距离d=
<1=r,
所以直线l与圆O相交.
直线l被圆O所截的弦长为L=2
=2
=2
=2
∵0≤m2≤4∴3≤
m2+3≤4,
≤
≤
,∴
≤L≤
.
| x2 |
| a2 |
| y2 |
| b2 |
由椭圆的定义知:2a=
(1+1)2+(
|
(1-1)2+(
|
得a=2,b=
| 3 |
故C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
解法二:设椭圆C的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
依题意,a2=b2+1①,将点M(1,
| 3 |
| 2 |
| 12 |
| a2 |
(
| ||
| b2 |
由①②解得a2=4,b2=3,故C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)因为点P(m,n)在椭圆C上运动,所以
| m2 |
| 4 |
| n2 |
| 3 |
| m2 |
| 4 |
| n2 |
| 3 |
从而圆心O到直线l:mx+ny=1的距离d=
| 1 | ||
|
所以直线l与圆O相交.
直线l被圆O所截的弦长为L=2
| 1-d2 |
1-
|
1-
|
1-
|
∵0≤m2≤4∴3≤
| 1 |
| 4 |
| 1 |
| 4 |
| 1 | ||
|
| 1 |
| 3 |
2
| ||
| 3 |
| 3 |
点评:解决此类问题关键是熟练掌握椭圆中的相关数值,灵活运用定义,待定系数等方法解决相关问题,利用直线与圆的位置关系求弦长的范围.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
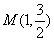 。
。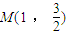 .
.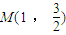 .
.