Question

叙述并正明三垂线定理（写出已知、求证及证明过程，并作图）

Answer 1

【答案】分析：三垂线定理内容为：在平面内的一直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直，画出满足条件的图形后，结合线面垂直的判定定理及性质，即可证明该定理．
解答：解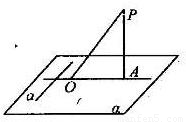：三垂线定理：在平面内的一直线，如果和这个平面的一条斜线的射影垂直，那么它
也和这条斜线垂直…（3分）
已知：如图PA、PO分别是平面α的垂线、斜线，AO是PO在平面α内的摄影，
证明如下：
∵a?α，a⊥AO
∵PA⊥α，a?α
∴PA⊥a，AO⊥a，PA∩AO=A
∴a⊥平面PAO，
又∵PO?平面PAO
∴a⊥PO…．（2分）
点评：三垂线定理及逆定理是二面角求解中最有用的工具之一，也是线线垂直证明的常用工具，虽然新课标教材中，没有要求掌握该定理，但三垂线定理易证，好用！还是希望大家了解！