题目内容
已知三个正整数2a,1,a2+3按某种顺序排列成等差数列.
(1)求a的值;
(2)若等差数列{an}的首项、公差都为a,等比数列{bn}的首项、公比也都为a,前n项和分别为Sn,Tn,且
>Sn-130,求满足条件的正整数n的最大值.
(1)求a的值;
(2)若等差数列{an}的首项、公差都为a,等比数列{bn}的首项、公比也都为a,前n项和分别为Sn,Tn,且
| Tn+2 | 2n |
分析:(1)利用2a,a2+3是正整数,可得a是正整数,利用基本不等式可得a2+3>2a>1,因此可得2a是a2+3与1的等差中项,即可得出;.
(2)利用a=2和等差数列、等比数列的前n项和公式即可得出.
(2)利用a=2和等差数列、等比数列的前n项和公式即可得出.
解答:解:(1)∵2a,a2+3是正整数,∴a是正整数,
∵a2+3>2a>1,
∴2×2a=a2+3+1,解得a=2.
(2)∵a=2,∴Sn=2n+
×2=n2+n;
Tn=
=2n+1-2,
∵
>Sn-130,∴
>n2+n-130,
化为n2+n-132<0,∴-12<n<11,
∵n是正整数,∴n的最大值是10.
∵a2+3>2a>1,
∴2×2a=a2+3+1,解得a=2.
(2)∵a=2,∴Sn=2n+
| n(n-1) |
| 2 |
Tn=
| 2(2n-1) |
| 2-1 |
∵
| Tn+2 |
| 2n |
| 2n+1-2+2 |
| 2n |
化为n2+n-132<0,∴-12<n<11,
∵n是正整数,∴n的最大值是10.
点评:熟练掌握等差数列、等比数列的前n项和公式及其通项公式是解题的关键.

练习册系列答案
相关题目
 >Sn-130,求满足条件的正整数n的最大值.
>Sn-130,求满足条件的正整数n的最大值.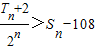 ,求满足条件的正整数n的最大值.
,求满足条件的正整数n的最大值. ,求满足条件的正整数n的最大值.
,求满足条件的正整数n的最大值.