题目内容
过抛物线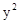 = 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )
= 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )
A.相交 B.相离 C.相切 D.不能确定
C
解析考点:圆与圆锥曲线的综合.
专题:综合题.
分析:设P为AB中点,A、B、P在准线l上射影分别为M、N、Q,根据抛物线的定义,可知AP+BP=AM+BN,从而 PQ= 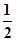 AB,所以以AB为直径作圆则此圆与准线l相切.
AB,所以以AB为直径作圆则此圆与准线l相切.
解答:解:设AB为过抛物线焦点F的弦,P为AB中点,A、B、P在准线l上射影分别为M、N、Q,
∵AP+BP=AM+BN
∴PQ=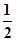 AB,
AB,
∴以AB为直径作圆则此圆与准线l相切
故选C.
点评:本题以抛物线为载体,考查抛物线过焦点弦的性质,关键是正确运用抛物线的定义,合理转化,综合性强.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
椭圆 的离心率为
的离心率为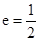 ,右焦点为
,右焦点为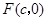 ,方程
,方程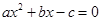 的两个实根分别为
的两个实根分别为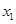 和
和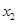 ,则点
,则点 ( )
( )
A.必在圆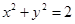 内 内 | B.必在圆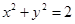 上 上 |
C.必在圆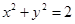 外 外 | D.以上三种情形都有可能 |
设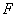 为抛物线
为抛物线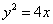 的焦点,
的焦点,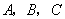 为该抛物线上三点,若
为该抛物线上三点,若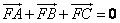 ,则
,则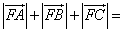
| A.9 | B.6 | C.4 | D.3 |
下列曲线中,与双曲线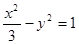 的离心率和渐近线都相同的是( )
的离心率和渐近线都相同的是( )
A.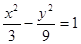 | B.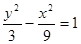 | C.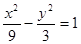 | D.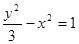 |
椭圆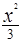 +
+ =1上一点P到左焦点的距离为
=1上一点P到左焦点的距离为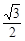 ,则P到右准线的距离为( )
,则P到右准线的距离为( )
A.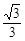 | B. | C.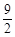 | D.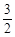 |
设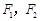 分别是双曲线
分别是双曲线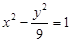 的左、右焦点.若点
的左、右焦点.若点 在双曲线上,且
在双曲线上,且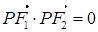 ,则
,则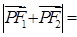
A.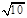 | B.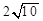 | C.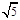 | D.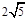 |
抛物线 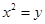 的准线方程是(***)
的准线方程是(***)
| A.4 x + 1 = 0 | B.4 y + 1 = 0 | C.2 x + 1 = 0 | D.2 y + 1 = 0 |
直线 经过椭圆
经过椭圆 的一个焦点和一个顶点,则该椭圆的离心率为.
的一个焦点和一个顶点,则该椭圆的离心率为.
A. | B. | C. | D. |
 上的两点,并且满足OA⊥OB.
上的两点,并且满足OA⊥OB.