题目内容
点M是边长为2的正方形ABCD内或边界上一动点,N是边BC的中点,则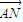 •
•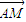 的最大值是( )
的最大值是( )A.2
B.4
C.5
D.6
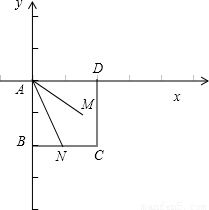
【答案】分析:以A为坐标原点,以AD方向为x轴正方向,在平面内建立合适的坐标系,将向量的数量积用坐标表示,再利用线性规划方法解决问题.
解答:解:以A为坐标原点,以AD方向为x轴正方向,
以AB方向为y轴负方向建立坐标系,则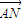 =(1,-2)
=(1,-2)
设M点坐标为(x,y),则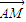 =(x,y),则0≤x≤2,-2≤y≤0
=(x,y),则0≤x≤2,-2≤y≤0
令Z=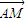 •
•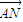 =x-2y,由题意可得Z的最大值在正方形的顶点处取得,
=x-2y,由题意可得Z的最大值在正方形的顶点处取得,
将A,B,C,D四点坐标依次代入得:ZA=0,ZB=4,ZC=6,ZD=2,故Z=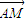 •
•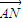 的最大值为6.
的最大值为6.
故选:D.
点评:本题主要考查两个向量的数量积公式的应用,向量的主要功能就是数形结合,将几何问题转化为代数问题,但关键是建立合适的坐标系,将向量用坐标表示,再将数量积运算转化为方程或函数问题.
解答:解:以A为坐标原点,以AD方向为x轴正方向,
以AB方向为y轴负方向建立坐标系,则
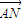 =(1,-2)
=(1,-2)设M点坐标为(x,y),则
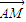 =(x,y),则0≤x≤2,-2≤y≤0
=(x,y),则0≤x≤2,-2≤y≤0令Z=
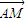 •
•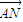 =x-2y,由题意可得Z的最大值在正方形的顶点处取得,
=x-2y,由题意可得Z的最大值在正方形的顶点处取得,将A,B,C,D四点坐标依次代入得:ZA=0,ZB=4,ZC=6,ZD=2,故Z=
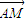 •
•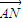 的最大值为6.
的最大值为6.故选:D.

点评:本题主要考查两个向量的数量积公式的应用,向量的主要功能就是数形结合,将几何问题转化为代数问题,但关键是建立合适的坐标系,将向量用坐标表示,再将数量积运算转化为方程或函数问题.

练习册系列答案
相关题目