题目内容
在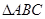 中,
中,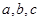 分别是角
分别是角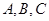 的对边,
的对边, ,
,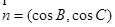 ,且
,且
(1)求角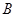 的大小;
的大小;
(2)设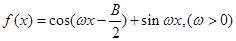 ,且
,且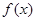 的最小正周期为
的最小正周期为 ,求
,求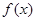 在
在 上的最大值和最小值,及相应的
上的最大值和最小值,及相应的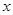 的值。
的值。
(1) (2)
(2) 时,
时, 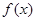 取得最大值
取得最大值 ;
; 时,
时, 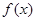 取得最小值
取得最小值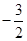 .
.
解析试题分析:(1)由 ,得
,得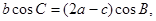
 ---2分
---2分
由正弦定理,得

又∵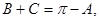
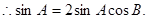 ---4分
---4分
又
又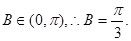 ---6分
---6分
(2)
由已知 ---8分
---8分
∴ ,
,
所以当 时,
时, ,
, ,
,
 当
当 ,即
,即 时,
时, 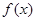 取得最大值
取得最大值 ; ---10分
; ---10分
当 即
即 时,
时, 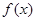 取得最小值
取得最小值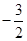 . ---12分
. ---12分
考点:本小题主要以向量为载体,考查用正弦定理和诱导公式解三角形以及三角函数的图象及最值问题,考查学生分析问题、解决问题的能力与运算能力.
点评:解三角形时,利用正弦定理有时比用余弦定理运算简单;考查三角函数的图象和性质时,要先把函数化成 的形式,并且注意其中参数的取值范围.
的形式,并且注意其中参数的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
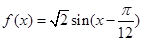 ,
,
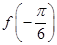 的值;
的值;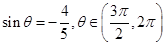 ,求
,求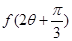 .
.
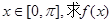 的最大值和最小值;
的最大值和最小值;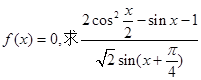 的值。
的值。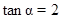 ,
, 的值;(Ⅱ)
的值;(Ⅱ)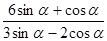 的值.
的值.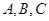 是
是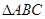 的三个内角,若向量
的三个内角,若向量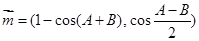 ,
,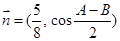 ,且
,且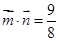 。
。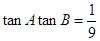 ; (2)求
; (2)求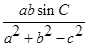 的最大值。
的最大值。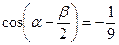 ,
,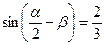 ;且
;且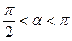 ,
,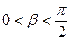
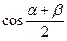
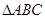 的内角A,B,C所对的边分别为a,b,c,若
的内角A,B,C所对的边分别为a,b,c,若 的可能取值为( ).
的可能取值为( ).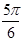
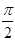
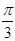
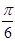
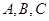 是三角形
是三角形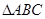 三内角,向量
三内角,向量 ,且
,且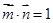 [.Com]
[.Com]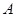 ; (2)若
; (2)若 ,求
,求 。
。 中,角
中,角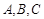 所对的边分别为
所对的边分别为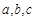 ,且
,且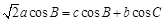
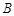 的大小;
的大小;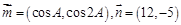 ,求当
,求当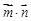 取最大值时,
取最大值时,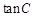 的值.
的值.