题目内容
已知函数 在点(1,f(1))处的切线方程为y = 2.
在点(1,f(1))处的切线方程为y = 2.
(I)求f(x)的解析式;
(II)设函数 若对任意的
若对任意的 ,总存唯一实数
,总存唯一实数 ,使得
,使得 ,求实数a的取值范围.
,求实数a的取值范围.
【答案】
(I)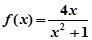 (II)
(II) 
【解析】
试题分析:(Ⅰ)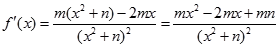 ……2分
……2分
由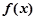 在点
在点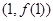 处的切线方程为
处的切线方程为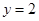 ,得
,得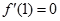 ,
,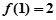
即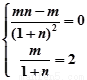 ,
, 解得
解得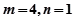 .故
.故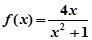 ……4分
……4分
(Ⅱ)由(Ⅰ)知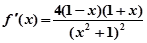 ,故
,故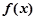 在
在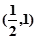 上单调递增,在
上单调递增,在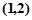
 上单调递减,由
上单调递减,由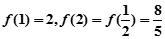 ,故
,故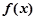 的值域为
的值域为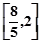 ……6分
……6分
依题意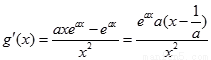 ,记
,记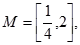
(ⅰ)当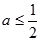 时,
时,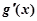
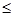
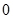 ,
,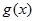 在
在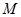 上单调递减,依题意由
上单调递减,依题意由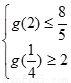 得
得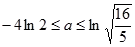 ,
,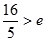 故此时
故此时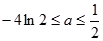 ……8分
……8分
(ⅱ)当 时,
时,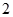 >
>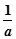 >
>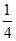 当
当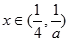 时,
时, <
<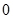 ,当
,当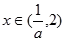 时,
时, >
>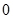 .依题意得:
.依题意得:
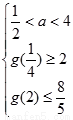 或
或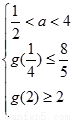 解得
解得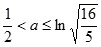 ……10分
……10分
(ⅲ)当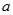
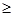 4时,
4时,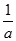
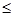
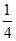 ,此时
,此时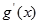 >
>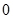 ,
,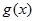 在
在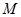 单调递增.依题意得
单调递增.依题意得
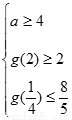 即
即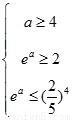 此不等式组无解 ……11分
此不等式组无解 ……11分
综上,所求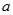 取值范围为
取值范围为 ……12分.
……12分.
考点:本小题主要考查利用导数研究函数的性质和参数范围的求解.
点评:导数是研究函数性质的有力工具,研究函数时,首先要看函数的定义域,求单调区间、极值、最值时,往往离不开分类讨论,主要考查学生的分类讨论思想的应用和运算求解能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
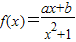 在点(-1,f(-1))的切线方程为x+y+3=0.
在点(-1,f(-1))的切线方程为x+y+3=0. 在点x=1处的切线与直线
在点x=1处的切线与直线 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值. 在点x=1处的切线与直线
在点x=1处的切线与直线 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值。
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值。 在点x=1处的切线与直线
在点x=1处的切线与直线 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值。
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值。