题目内容
一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为h1,h2,h,则h1:h2:h=分析:由题意画出图形,几何体是一个棱长都相等的斜三棱柱,四棱锥的高是P到AD的距离;三棱锥的高及三棱柱的高都是三棱锥的高;不难求得结果.
解答: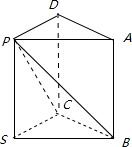 解:由题意作图如图,几何体是一个棱长都相等的斜三棱柱,
解:由题意作图如图,几何体是一个棱长都相等的斜三棱柱,
设棱长为1,四棱锥是棱长都相等的正四棱锥,三棱锥是一个正四面体
四棱锥的高是P到面AC的距离,P点到线段AD的距离是
,令P在底面AC上的身影为0,连接AO,则AO=
,故PO=
=
=
;
三棱锥的高就是P点到面SBC的距离,令P点在面SBC上的身影为M,则M是三角形的重心,故SM=
×
=
故PM=
=
=
;
三棱柱的高也是PM=
.
因而h1:h2:h=
:
:
=
:
:
故答案为:
:
:
 解:由题意作图如图,几何体是一个棱长都相等的斜三棱柱,
解:由题意作图如图,几何体是一个棱长都相等的斜三棱柱,设棱长为1,四棱锥是棱长都相等的正四棱锥,三棱锥是一个正四面体
四棱锥的高是P到面AC的距离,P点到线段AD的距离是
| ||
| 2 |
| ||
| 2 |
| PA2-AO2 |
12-(
|
| ||
| 2 |
三棱锥的高就是P点到面SBC的距离,令P点在面SBC上的身影为M,则M是三角形的重心,故SM=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
故PM=
| PS2-SM2 |
12-(
|
| ||
| 3 |
三棱柱的高也是PM=
| ||
| 3 |
因而h1:h2:h=
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
故答案为:
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
点评:本题考查简单几何体的有关知识,考查空间想象能力,考查同学的想图、视图能力,是基础题.

练习册系列答案
相关题目