题目内容
 设双曲线
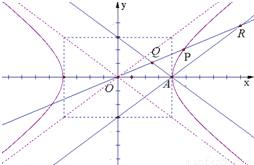
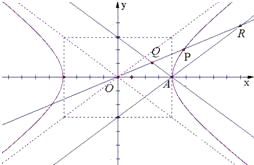
设双曲线 -y2=1的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP (O为坐标原点)分别交于Q和R两点.
-y2=1的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP (O为坐标原点)分别交于Q和R两点.
(1)证明:无论P点在什么位置,总有| |2=|
|2=|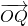 •
•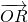 |;
|;
(2)设动点C满足条件: =
= (
(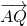 +
+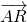 ),求点C的轨迹方程.
),求点C的轨迹方程.
解:(1)设OP:y=kx与AR:y=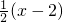 联立,解得
联立,解得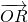 =
=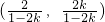 ,
,
同理可得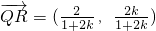 ,所以|
,所以|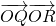 |=
|=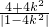 ,
,
设 =(m,n),则由双曲线方程与OP方程联立解得
=(m,n),则由双曲线方程与OP方程联立解得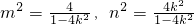 ,
,
所以| |2=
|2=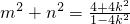 =|
=|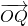 •
•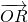 |(点在双曲线上,1-4k2>0);
|(点在双曲线上,1-4k2>0);
(2)∵ =
= (
(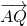 +
+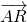 ),
),
∴点C为QR的中点,设C(x,y),
则有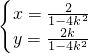 ,消去k,可得所求轨迹方程为x2-2x-4y2=0(x≠0).
,消去k,可得所求轨迹方程为x2-2x-4y2=0(x≠0).
分析:(1)设OP:y=kx与AR:y=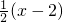 联立,解得
联立,解得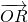 =
=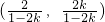 ,同理可得
,同理可得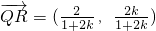 ,所以|
,所以|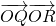 |=
|=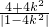 ,由此知|
,由此知| |2=
|2=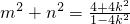 =|
=|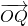 •
•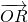 |.
|.
(2)由 =
= (
(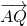 +
+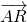 ),知点C为QR的中点,设C(x,y),有
),知点C为QR的中点,设C(x,y),有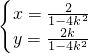 ,消去k,可得所求轨迹方程.
,消去k,可得所求轨迹方程.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意合理地进行等价转化.
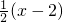 联立,解得
联立,解得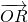 =
=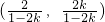 ,
,同理可得
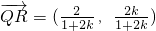 ,所以|
,所以|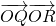 |=
|=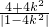 ,
, 设
 =(m,n),则由双曲线方程与OP方程联立解得
=(m,n),则由双曲线方程与OP方程联立解得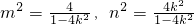 ,
,所以|
 |2=
|2=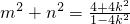 =|
=|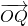 •
•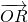 |(点在双曲线上,1-4k2>0);
|(点在双曲线上,1-4k2>0);(2)∵
 =
= (
(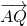 +
+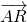 ),
),∴点C为QR的中点,设C(x,y),
则有
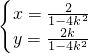 ,消去k,可得所求轨迹方程为x2-2x-4y2=0(x≠0).
,消去k,可得所求轨迹方程为x2-2x-4y2=0(x≠0).分析:(1)设OP:y=kx与AR:y=
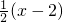 联立,解得
联立,解得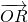 =
=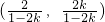 ,同理可得
,同理可得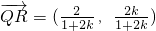 ,所以|
,所以|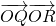 |=
|=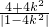 ,由此知|
,由此知| |2=
|2=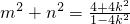 =|
=|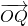 •
•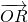 |.
|.(2)由
 =
= (
(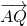 +
+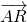 ),知点C为QR的中点,设C(x,y),有
),知点C为QR的中点,设C(x,y),有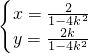 ,消去k,可得所求轨迹方程.
,消去k,可得所求轨迹方程.点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目
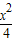 -y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2
-y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2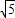 ,y≥0)上的点,线段|PkF|的长度为ak,(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈(
,y≥0)上的点,线段|PkF|的长度为ak,(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈( ,
,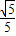 ),则n最大取值为 .
),则n最大取值为 .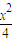 -y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2
-y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2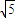 ,y≥0)上的点,线段|PkF|的长度为ak,(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈(
,y≥0)上的点,线段|PkF|的长度为ak,(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈(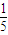 ,
,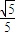 ),则n最大取值为 .
),则n最大取值为 .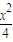 -y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2
-y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2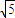 ,y≥0)上的点,线段|PkF|的长度为ak,(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈(
,y≥0)上的点,线段|PkF|的长度为ak,(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈(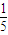 ,
,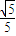 ),则n最大取值为 .
),则n最大取值为 .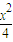 -y2=1的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP (O为坐标原点)分别交于Q和R两点.
-y2=1的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP (O为坐标原点)分别交于Q和R两点.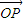 |2=|
|2=|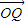 •
•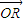 |;
|;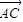 =
= (
(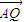 +
+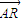 ),求点C的轨迹方程.
),求点C的轨迹方程.