题目内容
已知
,
,
为平面向量,命题p:若λ
=
(λ为实数),则λ必为0;命题q:若
•
=
•
,则
=
.对以上两个命题,下列结论中正确的是( )
| a |
| b |
| c |
| a |
| 0 |
| a |
| c |
| b |
| c |
| a |
| b |
分析:分别对命题p、q进行真假判断,而后对复合命题判断真假可得到答案.
解答:解:“若λ
=
(λ为实数),则λ必为0”为假命题,
∵
=
也符合要求,即命题p为假命题.
又∵
•
=|
|•
|•cosα,
•
=|
| •|
| •cosβ,
若
•
=
•
,则有|
| •|
| •cosα=|
|•|
| •cosβ,
上式成立,未必有
=
,
∴命题q为假命题.
由上可得:命题“p且q”为假命题,
命题“p或q”为假命题,
命题“p或¬q”为真命题,
命题“¬p”或“¬q”为真命题.
故选A.
| a |
| 0 |
∵
| a |
| 0 |
又∵
| a |
| c |
| a |
| c |
| b |
| c |
| b |
| c |
若
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| c |
上式成立,未必有
| a |
| b |
∴命题q为假命题.
由上可得:命题“p且q”为假命题,
命题“p或q”为假命题,
命题“p或¬q”为真命题,
命题“¬p”或“¬q”为真命题.
故选A.
点评:本题以向量为载体,考查简单命题、复合命题的真假判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知A,B,C为平面上不共线的三点,若向量
=(1,1),
=(1,-1),且
•
=2,则
•
等于( )
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A、-2 | B、2 | C、0 | D、2或-2 |
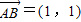 ,
,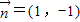 ,且
,且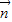 •
•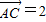 ,则
,则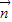 •
•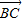 等于( )
等于( )