题目内容
已知对任意平面向量![]() ,把
,把![]() 绕其起点沿逆时针方向旋转q角得到向量
绕其起点沿逆时针方向旋转q角得到向量![]() ,叫做把点B绕点A逆时针方向旋转q角得到点P.
,叫做把点B绕点A逆时针方向旋转q角得到点P.
(1)已知平面内点A(2,1),点B(![]() ,
,![]() ).把点B绕点A沿逆时针方向旋转
).把点B绕点A沿逆时针方向旋转![]() 后得到点P,求点P的坐标;
后得到点P,求点P的坐标;
(2)设平面内曲线C上的每一点绕坐标原点O沿顺时针方向旋转![]() 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线![]() ,求原来曲线C的方程.
,求原来曲线C的方程.
解:
(1) 设P(x,y), 则![]() ,
,
![]() ,
,
由题意,得:
![]()
∴ x-2=6,y-1=2, ∴x=8,y=3.
(2)设P(x,y)是曲线C上任意一点,![]() 绕绕坐标原点O沿顺时针方向旋转
绕绕坐标原点O沿顺时针方向旋转![]() 后,点P的坐标为(x’,y’),则:
后,点P的坐标为(x’,y’),则:
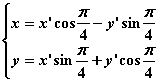 即
即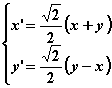
又因为![]() 所以
所以 ![]()
化简得: ![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 =(x,y),把
=(x,y),把 角得到向量
角得到向量 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 后得到点的轨迹是曲线
后得到点的轨迹是曲线 ,则原来曲线C的方程是____
,则原来曲线C的方程是____