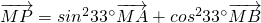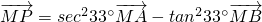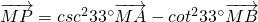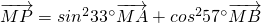题目内容
下列条件中,不能确定三点A、B、P共线的是( )A.
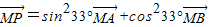
B.
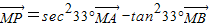
C.
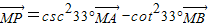
D.
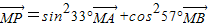
【答案】分析:利用三角函数的平方关系及向量的三角形法则、向量共线的充要条件,判断出A,B,C都能确定三点A、B、P共线,
由三角函数的平方关系得到D为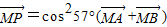 ,所以能确定三点A、B、P共线.
,所以能确定三点A、B、P共线.
解答:解:对于A,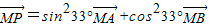 即为
即为
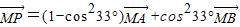
即为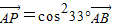 ,所以能确定三点A、B、P共线;
,所以能确定三点A、B、P共线;
对于B,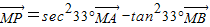 即为
即为
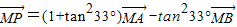 即为
即为 ,所以确定三点A、B、P共线
,所以确定三点A、B、P共线
对于C,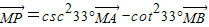 即为
即为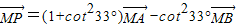 ,
,
即为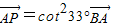 ,所以确定三点A、B、P共线;
,所以确定三点A、B、P共线;
对于D,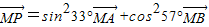 即
即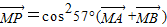 ,所以不能确定三点A、B、P共线.
,所以不能确定三点A、B、P共线.
故选D.
点评:本题考查三角函数的平方关系、向量的三角形法则及向量共线的充要条件,是一道基础题.
由三角函数的平方关系得到D为
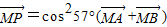 ,所以能确定三点A、B、P共线.
,所以能确定三点A、B、P共线.解答:解:对于A,
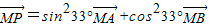 即为
即为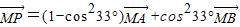
即为
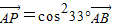 ,所以能确定三点A、B、P共线;
,所以能确定三点A、B、P共线;对于B,
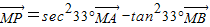 即为
即为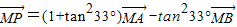 即为
即为 ,所以确定三点A、B、P共线
,所以确定三点A、B、P共线对于C,
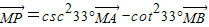 即为
即为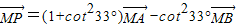 ,
,即为
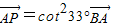 ,所以确定三点A、B、P共线;
,所以确定三点A、B、P共线;对于D,
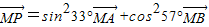 即
即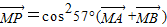 ,所以不能确定三点A、B、P共线.
,所以不能确定三点A、B、P共线.故选D.
点评:本题考查三角函数的平方关系、向量的三角形法则及向量共线的充要条件,是一道基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目