题目内容
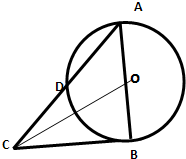 如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠ACO=
如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠ACO=分析:根据切线的性质,我们易判断△ABC为Rt△,结合圆周角定理的推论2及AD=DC,及得△ABC为等腰直角三角形,则∠BCA=45°,设圆的半径为1,则我们易求出∠OCB的三角函数值,代入两角差的正弦公式,即可求出答案.
解答:解:∵AB为直径,BC为圆的切线
且AD=DC
∴△ABC为等腰直角三角形,
设圆的半径为1,则OB=1,BC=2,0C=
∴sin∠BC0=
,cos∠BC0=
∴sin∠ACO=sin(45°-∠BCO)=
故答案为:
且AD=DC
∴△ABC为等腰直角三角形,
设圆的半径为1,则OB=1,BC=2,0C=
| 5 |
∴sin∠BC0=
| ||
| 5 |
2
| ||
| 5 |
∴sin∠ACO=sin(45°-∠BCO)=
| ||
| 10 |
故答案为:
| ||
| 10 |
点评:本题考查的知识点是圆的切线的性质定理,圆周角定理,其中根据已知判断出△ABC的形状,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
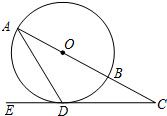 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30度.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30度. 15、如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是
15、如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是
 (2011•惠州模拟)如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠BCO=
(2011•惠州模拟)如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠BCO= 如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙O于E点,若AE平分
如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙O于E点,若AE平分