题目内容
已知向量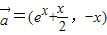 ,
,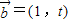 ,若函数
,若函数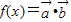 在区间(-1,1)上存在单调递增区间,则t的取值范围是 .
在区间(-1,1)上存在单调递增区间,则t的取值范围是 .
【答案】分析:先根据平面向量的数量积公式求出函数f(x)的解析式,欲使函数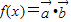 在区间(-1,1)上存在单调递增区间
在区间(-1,1)上存在单调递增区间
即使f′(x)>0在区间(-1,1)上有解即可.
解答:解: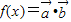 =
=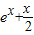 -tx
-tx
则f′(x)=ex+( -t)
-t)
∵函数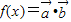 在区间(-1,1)上存在单调递增区间
在区间(-1,1)上存在单调递增区间
∴f′(x)=ex+( -t)>0在区间(-1,1)上有解
-t)>0在区间(-1,1)上有解
即t<ex+ 在区间(-1,1)上有解
在区间(-1,1)上有解
而在区间(-1,1)上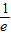 +
+ <ex+
<ex+ <e+
<e+
∴t<e+
故答案为:(-∞,e+ )
)
点评:本题主要考查了平面向量数量积的运算,同时考查了转化的思想和运算求解的能力,属于中档题.
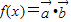 在区间(-1,1)上存在单调递增区间
在区间(-1,1)上存在单调递增区间即使f′(x)>0在区间(-1,1)上有解即可.
解答:解:
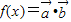 =
=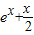 -tx
-tx则f′(x)=ex+(
 -t)
-t)∵函数
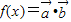 在区间(-1,1)上存在单调递增区间
在区间(-1,1)上存在单调递增区间∴f′(x)=ex+(
 -t)>0在区间(-1,1)上有解
-t)>0在区间(-1,1)上有解即t<ex+
 在区间(-1,1)上有解
在区间(-1,1)上有解而在区间(-1,1)上
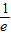 +
+ <ex+
<ex+ <e+
<e+
∴t<e+

故答案为:(-∞,e+
 )
)点评:本题主要考查了平面向量数量积的运算,同时考查了转化的思想和运算求解的能力,属于中档题.

练习册系列答案
相关题目
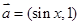 ,
,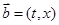 ,若函数
,若函数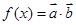 在区间
在区间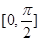 上是增函数,则实数
上是增函数,则实数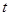 的取值范围是_________.
的取值范围是_________. ,
, ,若函数
,若函数 在区间(-1,1)上存在单调递增区间,则t的取值范围是 .
在区间(-1,1)上存在单调递增区间,则t的取值范围是 .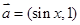 ,
,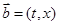 ,若函数
,若函数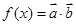 在区间
在区间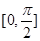 上是增函数,则实数
上是增函数,则实数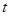 的取值范围是_________.
的取值范围是_________. ,
, ,若函数
,若函数
 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围是 ( )
的取值范围是 ( ) (B)
(B) (C)
(C) (C)
(C)