题目内容
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
| 组别 | 候车时间 | 人数 |
| 一 |  | 2 |
| 二 |  | 6 |
| 三 |  | 4 |
| 四 |  | 2 |
| 五 |  | 1 |
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
(1)32;(2)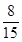 .
.
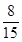 .
.试题分析:(1)用候车时间少于10分钟的总人数除以15,得到的频率再乘以60;(2)先计算从三、四两组中任选2人的基本事件个数,为此,将第三组乘客编号为
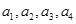 ,第四组乘客编号为
,第四组乘客编号为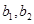 ,选中
,选中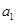 的事件有
的事件有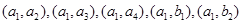 共5个,未选中
共5个,未选中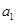 而选中
而选中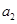 的事件有
的事件有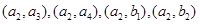 共4个,
共4个,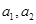 都未选中而选中
都未选中而选中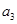 的事件有
的事件有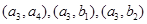 共3个,
共3个, 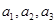 都未选中而选中
都未选中而选中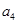 的事件有
的事件有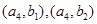 共2个,选中的两人都来自四组的事件为
共2个,选中的两人都来自四组的事件为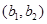 共1个,所以共15个基本事件,其中2人恰好来自不同组的事件有
共1个,所以共15个基本事件,其中2人恰好来自不同组的事件有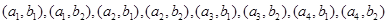 共8个,后者除以前者即得
共8个,后者除以前者即得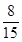 .
.试题解析:(1)候车时间少于10分钟的概率为
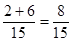 , 4分
, 4分所以候车时间少于10分钟的人数为
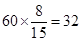 人; 6分
人; 6分(2)将第三组乘客编号为
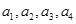 ,第四组乘客编号为
,第四组乘客编号为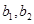 .从6人中任选两人有包含以下基本事件:
.从6人中任选两人有包含以下基本事件: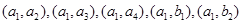 ,
,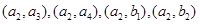 ,
,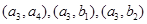 ,
,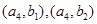 ,
,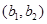 共15个基本事件, 10分
共15个基本事件, 10分其中两人恰好来自不同组包含8个基本事件,所以所求概率为
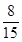 . 12分
. 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 三所不同的中学抽取60名教师进行调查.已知
三所不同的中学抽取60名教师进行调查.已知 学校中应抽取的人数为( ).
学校中应抽取的人数为( ).