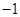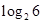题目内容
已知定义在R上的奇函数 满足
满足 ,则
,则 的值为
的值为
 满足
满足 ,则
,则 的值为
的值为| A.-1 | B.0 | C.1 | D.2 |
B
由f(x+2)=-f(x)知,f(x+4)=f [(x+2)+2]=-f(x+2)=f(x),
∴f(6)=f(4+2)=f(2)=f(0+2)=-f(0).又由f(x)为R上的奇函数知f(0)=0,
∴f(6)=-f(0)=0.故选B.
∴f(6)=f(4+2)=f(2)=f(0+2)=-f(0).又由f(x)为R上的奇函数知f(0)=0,
∴f(6)=-f(0)=0.故选B.

练习册系列答案
相关题目
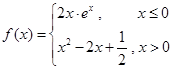 ,给出下列命题:①过该函数图象上一点
,给出下列命题:①过该函数图象上一点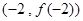 的切
的切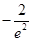 ;②函数
;②函数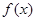 的最小值等于
的最小值等于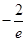 ;③该方程
;③该方程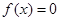 有四个不同的实数根;④函数
有四个不同的实数根;④函数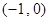 以及
以及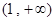 上都是增函数,其中正确命题的个数是( )
上都是增函数,其中正确命题的个数是( )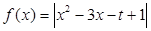 在区间
在区间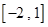 上的最大值为2,则实数
上的最大值为2,则实数 ▲ .
▲ .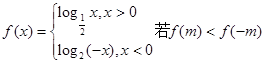 ,则实数m的取值范围是()
,则实数m的取值范围是()



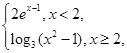
 则不等式f(x)>2的解集为 。
则不等式f(x)>2的解集为 。 上的函数
上的函数 满足
满足 ,
,  ,则有
,则有
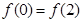

 关系不确定
关系不确定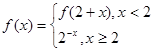 ,则
,则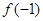 的值为
的值为 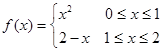 的图像与x轴所围成的封闭图形的面积为 .
的图像与x轴所围成的封闭图形的面积为 .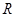 上的函数
上的函数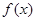 满足
满足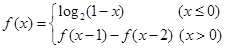 ,则
,则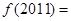 ( )
( )