题目内容
(1)
已知函数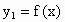 是单调递增的奇函数,定义域为[-1,1],求函数
是单调递增的奇函数,定义域为[-1,1],求函数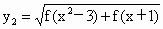 的定义域和值域.
的定义域和值域.
(2)
证明:函数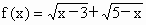 在区间[4,5]上是减函数.
在区间[4,5]上是减函数.
答案:略
解析:
解析:
|
解: (1)要使函数有意义须使 ∵f(x)为奇数,∴f(x+1)=f[-(x+1)].∴ ∵f(x)为奇数,∴f(x+1)=f[-(x+1)].∴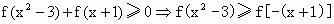 . .
又∵ f(x)定义域为[-1,1]且为增函数,∴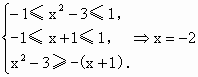 . .
∴函数的定义域为 {-2},值域为{0}.(2) 证明:设 ,则 ,则
∵  ∴ ∴ , ,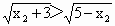 则 则 . . ,又 ,又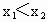 ,∴ ,∴ 即 即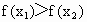 ,∴f(x)在区间[4,5]上是减函数. ,∴f(x)在区间[4,5]上是减函数. |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

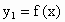 是单调递增的奇函数,定义域为[-1,1],求函数
是单调递增的奇函数,定义域为[-1,1],求函数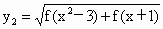 的定义域和值域.
的定义域和值域.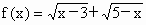 在区间[4,5]上是减函数.
在区间[4,5]上是减函数.