题目内容
选修4-4:作标系与参数方程
(1)已知点C 的极坐标为(2,
),画图并求出以C为圆心,半径r=2的圆的极坐标
方程(写出解题过程);
(2)P是以原点为圆心,r=2的圆上的任意一点,Q(6,0),M是PQ中点
①画图并写出⊙O的参数方程;
②当点P在圆上运动时,求点M的轨迹的参数方程.
(1)已知点C 的极坐标为(2,
| π | 3 |
方程(写出解题过程);
(2)P是以原点为圆心,r=2的圆上的任意一点,Q(6,0),M是PQ中点
①画图并写出⊙O的参数方程;
②当点P在圆上运动时,求点M的轨迹的参数方程.
分析:(1)设M(ρ,θ),则∠MQC=θ-
或
-θ,由余弦定理能求出QC的极坐标方程.
(2)①⊙O的参数方程
.
②设M(x,y),P(2cosθ,2sinθ),因Q(6,0),能求出M的参数方程.
| π |
| 3 |
| π |
| 3 |
(2)①⊙O的参数方程
|
②设M(x,y),P(2cosθ,2sinθ),因Q(6,0),能求出M的参数方程.
解答:解: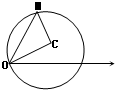 (1)如图,设M(ρ,θ)
(1)如图,设M(ρ,θ)
则∠MQC=θ-
或
-θ,
由余弦定理得4+ρ2-4cos(θ-
)=4,
∴QC的极坐标方程为ρ=4cos(θ-
)
(2)如图①⊙O的参数方程
,
②设M(x,y),P(2cosθ,2sinθ),
因Q(6,0)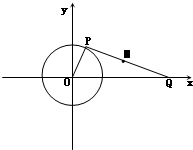
∴M的参数方程为
,
即
.
 (1)如图,设M(ρ,θ)
(1)如图,设M(ρ,θ)则∠MQC=θ-
| π |
| 3 |
| π |
| 3 |
由余弦定理得4+ρ2-4cos(θ-
| π |
| 3 |
∴QC的极坐标方程为ρ=4cos(θ-
| π |
| 3 |
(2)如图①⊙O的参数方程
|
②设M(x,y),P(2cosθ,2sinθ),
因Q(6,0)

∴M的参数方程为
|
即
|
点评:本题考查简单曲线的极坐标方程及其应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
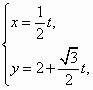 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为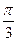 ),画图并求出以C为圆心,半径r=2的圆的极坐标
),画图并求出以C为圆心,半径r=2的圆的极坐标 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。
 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线

 的图象;
的图象; 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。
 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线

 的图象;
的图象; 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。