题目内容
5、已知平面α∩β=l,m是α内不同于l的直线,那么下列命题中错误 的是( )
分析:由题设条件,平面α∩β=l,m是α内不同于l的直线,结合四个选项中的条件,对结论进行证明,找出不能推出结论的即可
解答:解:A选项是正确命题,由线面平行的性质定理知,可以证出线线平行;
B选项是正确命题,因为两个平面相交,一个面中平行于它们交线的直线必平行于另一个平面;
C选项是正确命题,因为一个线垂直于一个面,则必垂直于这个面中的直线;
D选项是错误命题,因为一条直线垂直于一个平面中的一条直线,不能推出它垂直于这个平面;
综上D选项中的命题是错误的
故选D
B选项是正确命题,因为两个平面相交,一个面中平行于它们交线的直线必平行于另一个平面;
C选项是正确命题,因为一个线垂直于一个面,则必垂直于这个面中的直线;
D选项是错误命题,因为一条直线垂直于一个平面中的一条直线,不能推出它垂直于这个平面;
综上D选项中的命题是错误的
故选D
点评:本题考查空间中直线与平面之间的位置关系,解题的关键是有着较强的空间想像能力以及熟练掌握点线面位置关系判断的一些定义,定理及条件,并能灵活组织这些材料作出证明,故也考查了推理论证的能力.

练习册系列答案
相关题目
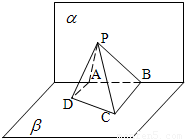
 (2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则P-ABCD体积的最大值是( )
(2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则P-ABCD体积的最大值是( ) (2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB面积的最大值是( )
(2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB面积的最大值是( )