题目内容
设曲线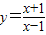 在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )A.2
B.

C.
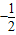
D.-2
【答案】分析:(1)求出已知函数y在点(3,2)处的斜率;(2)利用两条直线互相垂直,斜率之间的关系k1•k2=-1,求出未知数a.
解答:解:∵y= ∴y′=-
∴y′=-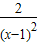
∵x=3∴y′=- 即切线斜率为-
即切线斜率为-
∵切线与直线ax+y+1=0垂直
∴直线ax+y+1=0的斜率为2.
∴-a=2即a=-2
故选D.
点评:函数y=f(x)在x=x处的导数的几何意义,就是曲线y=f(x)在点P(x,y)处的切线的斜率,过点P的切线方程为:y-y=f′(x)(x-x)
解答:解:∵y=
 ∴y′=-
∴y′=-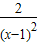
∵x=3∴y′=-
 即切线斜率为-
即切线斜率为-
∵切线与直线ax+y+1=0垂直
∴直线ax+y+1=0的斜率为2.
∴-a=2即a=-2
故选D.
点评:函数y=f(x)在x=x处的导数的几何意义,就是曲线y=f(x)在点P(x,y)处的切线的斜率,过点P的切线方程为:y-y=f′(x)(x-x)

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则a=( )
垂直,则a=( ) D.
D. 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则
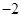 C.
C.
 D.
D.

 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则
 C.
C.
 D.
D.

 在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )

 在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
