题目内容
如图,在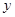 轴右侧的动圆⊙
轴右侧的动圆⊙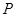 与⊙
与⊙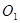 :
: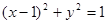 外切,并与
外切,并与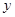 轴相切.
轴相切.
(Ⅰ)求动圆的圆心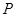 的轨迹
的轨迹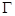 的方程;
的方程;
(Ⅱ)过点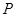 作⊙
作⊙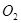 :
: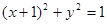 的两条切线,分别交
的两条切线,分别交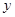 轴于
轴于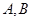 两点,设
两点,设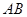 中点为
中点为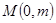 .求
.求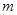 的取值范围.
的取值范围.

【答案】
(Ⅰ)由题意,点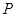 到点
到点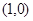 的距离等于它到直线
的距离等于它到直线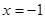 的距离,故
的距离,故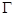 是抛物线,方程为
是抛物线,方程为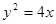 (
( ).…………………………………
).…………………………………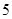 分
分
注:由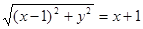 化简同样给分;不写
化简同样给分;不写 不扣分.
不扣分.
(Ⅱ)设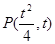 (
(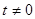 ),切线斜率为
),切线斜率为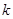 , 则切线方程为
, 则切线方程为 ,即
,即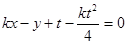 .…………………………
.…………………………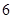 分
分
由题意, 的圆心
的圆心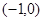 到切线的距离
到切线的距离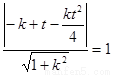 ,…………………………
,………………………… 分
分
两边平方并整理得: .……………………
.……………………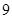 分
分
该方程的两根
 就是两条切线的斜率,由韦达定理:
就是两条切线的斜率,由韦达定理: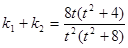 . ①
. ①
另一方面,在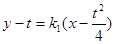 ,
,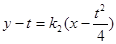 中
中 令
令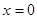 可得
可得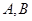 两点的纵坐标
两点的纵坐标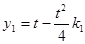 ,
,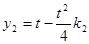 ,故
,故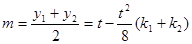 , ②
, ②
将①代入②,得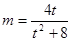
 ,……………………………
,…………………………… 分
分
故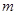 的取值范围是
的取值范围是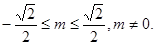
【解析】略

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 (2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D:
(2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D: 。椭圆D:
。椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

 与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线
与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线 斜率的范围。
斜率的范围。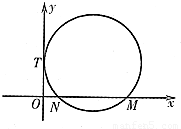 如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D:
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D: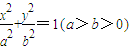 的焦距等于2|ON|,且过点
的焦距等于2|ON|,且过点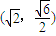 .
. 如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D:
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D: 的焦距等于2|ON|,且过点
的焦距等于2|ON|,且过点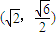 .
.