题目内容
等差数列 的前n项和为
的前n项和为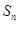 ,且
,且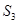 =6,
=6,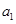 =4,则公差d等于( )
=4,则公差d等于( )
| A.1 | B.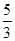 | C.- 2 | D.3 |
C
解析试题分析:方法一:基本量法.设等差数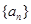 的公差为
的公差为 ,则
,则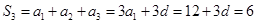 ,
,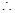
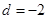 .
.
方法二:利用等差数列的性质.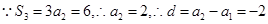 .
.
考点:等差数列基本量的计算

练习册系列答案
相关题目
设数列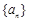 和
和 分别为等差数列与等比数列,且
分别为等差数列与等比数列,且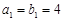 ,
, ,则以下结论正确的是( )
,则以下结论正确的是( )
A.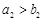 | B.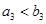 | C. | D.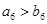 |
数列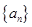 中,
中,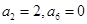 且数列
且数列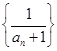 是等差数列,则
是等差数列,则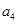 =( )
=( )
A. | B.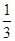 | C.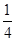 | D.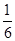 |
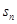 是等差数列
是等差数列 {
{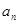 }的前n项和,
}的前n项和, ,
,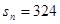 ,
,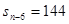 (n>6),则n等于 ( )
(n>6),则n等于 ( )
| A.15 | B.16 | C.17 | D.18 |
已知等比数列{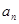 }中,各项都是正数,且
}中,各项都是正数,且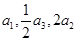 成等差数列,则
成等差数列,则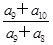 =( )
=( )
A.1- | B.1+ | C.3-2 | D.3+2 |
正项等比数列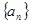 满足
满足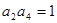 ,
,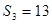 ,
, ,则数列
,则数列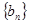 的前10项和是( ).
的前10项和是( ).
| A.65 | B.-65 | C.25 | D.-25 |
等差数列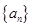
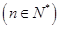 中,已知
中,已知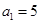 ,且在前
,且在前 项和
项和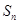 中,仅当
中,仅当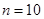 时,
时,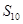 最大,则公差d满足( )
最大,则公差d满足( )
A.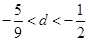 | B.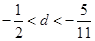 |
C.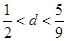 | D.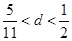 |
已知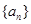 为等差数列,其前
为等差数列,其前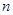 项和为
项和为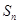 ,若
,若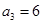 ,
,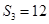 ,则公差
,则公差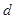 等于( )
等于( )
A. | B.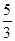 | C. | D. |
如果等差数列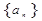 中,
中, ,那么
,那么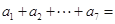 ( )
( )
| A.14 | B.21 | C.28 | D.35 |