题目内容
已知以F1(-2,0),F2(2,0)为焦点的椭圆与直线x+
y+4=0有且仅有一个交点,则椭圆的长轴长为( )
| 3 |
A、3
| ||
B、2
| ||
C、2
| ||
D、4
|
分析:由题设条件可以求出椭圆的方程是
+
=1.再把椭圆和直线联立方程组,由要根的判别式△=0能够求出a的值,从而能够求出椭圆的长轴长.
| x2 |
| a2 |
| y2 |
| a2-4 |
解答:解:设椭圆长轴长为2a(且a>2),则椭圆方程为
+
=1.
由,
得(4a2-12)y2+8
(a2-4)y+(16-a2)(a2-4)=0.
∵直线与椭圆只有一个交点,∴△=0,即192(a2-4)2-16(a2-3)×(16-a2)×(a2-4)=0.
解得a=0(舍去),a=2(舍去),a=
.∴长轴长2a=2
.故选C.
| x2 |
| a2 |
| y2 |
| a2-4 |
由,
|
| 3 |
∵直线与椭圆只有一个交点,∴△=0,即192(a2-4)2-16(a2-3)×(16-a2)×(a2-4)=0.
解得a=0(舍去),a=2(舍去),a=
| 7 |
| 7 |
点评:本题考查椭圆的基本知识及其应用,解题时要注意a>2这个前提条件,不要产生增根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 y+4=0有且仅有一个交点,则椭圆的长轴长为( )
y+4=0有且仅有一个交点,则椭圆的长轴长为( )



 y+4=0有且仅有一个交点,则椭圆的长轴长为( )
y+4=0有且仅有一个交点,则椭圆的长轴长为( )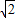



 y+4=0有且仅有一个交点,则椭圆的长轴长为( )
y+4=0有且仅有一个交点,则椭圆的长轴长为( )


