Question

（本题12分）投掷一个质地均匀，每个面上标有一个数字的正方体玩具，它的六个面中，有两个面的数字是，两个面的数字是2，两个面的数字是4.将此玩具连续抛掷两次，以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.

（1）求点P落在区域上的概率；

（2）若以落在区域上的所有点为顶点作面积最大的多边形区域M，在区域C上随机撒一粒豆子，求豆子落在区域M上的概率.

 

Answer 1

【答案】

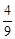（1）；（2） .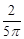

【解析】（1）先求出点P的坐标，然后再判断出落入圆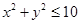内的点的个数.

最后根据古典概型概率计算公式计算即可.

(2)本小题属于几何概型概率，应先计算出区域M的面积，再算出事件发生的区域C的面积，然后面积相除即可.

解：（1）点P坐标有：（0，0），（0，2），（0，4），（2，0），（2，2），（2，4），（4，0），（4，2），（4，4），共9种，其中落在区域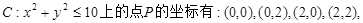

共4种.故点P落在区域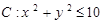上的概率为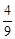…………6分             

（2）区域M为一边长为2的正方形，其面积为4，区域C的面积为10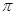，则豆子落在区域M上的概率为 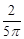. …………12分