题目内容
某商店进货每件50元，据市场调查，销售价格（每件x元）在50≤x≤80时，每天售出的件数P=
．若想每天获得的利润最多，销售价格每件应定为多少元？
【答案】分析：先依据题意设养殖加工生产业投入x万元，则养殖业投入为80-x万元，再利用x的函数式表示出年利润W，最后利用二次函数的值域求出其最大值，从而问题解决．
解答：解：设销售价格每件x元（50≤x≤80），每天获利润y元，
则y=（x-50）P=
（50≤x≤80）
问题转化为考虑u=
（50≤x≤80）的最大值即可．（5分）
这是一个u关于
的二次函数，
当
，即x=60∈[50，80]时，u取得最大值，
故每件定价为60元时，利润最大为：2500元．
点评：本小题主要考查函数模型的选择与应用、函数最值的应用等基础知识，解决实际问题通常有四个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果；（4）转译成具体问题作出解答，其中关键是建立数学模型．
解答：解：设销售价格每件x元（50≤x≤80），每天获利润y元，
则y=（x-50）P=
（50≤x≤80）问题转化为考虑u=
（50≤x≤80）的最大值即可．（5分）这是一个u关于的二次函数，当
，即x=60∈[50，80]时，u取得最大值，故每件定价为60元时，利润最大为：2500元．
点评：本小题主要考查函数模型的选择与应用、函数最值的应用等基础知识，解决实际问题通常有四个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果；（4）转译成具体问题作出解答，其中关键是建立数学模型．
练习册系列答案
相关题目
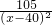．若想每天获得的利润最多，销售价格每件应定为多少元？