题目内容
(13分)定义在R上的增函数y=f(x)对任意x,y R都有f(x+y)=f(x)+f(y),则
R都有f(x+y)=f(x)+f(y),则
(1)求f(0) (2) 证明:f(x)为奇函数
(3)若 对任意
对任意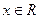 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
 R都有f(x+y)=f(x)+f(y),则
R都有f(x+y)=f(x)+f(y),则(1)求f(0) (2) 证明:f(x)为奇函数
(3)若
 对任意
对任意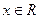 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围解:(1)f (0)=0…………………3分
(2) 令y=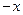 ,得f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x),即可证得………7分
,得f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x),即可证得………7分
(3)因为f(x)在R上时增函数,又由(2)知f(x)是奇函数,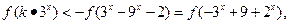 即有
即有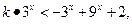 得
得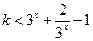 ,又有
,又有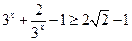 ,所以只要使
,所以只要使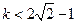 ………13分
………13分
(2) 令y=
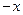 ,得f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x),即可证得………7分
,得f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x),即可证得………7分(3)因为f(x)在R上时增函数,又由(2)知f(x)是奇函数,
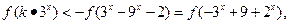 即有
即有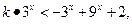 得
得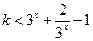 ,又有
,又有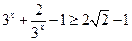 ,所以只要使
,所以只要使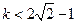 ………13分
………13分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
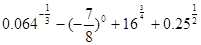 (2) 若
(2) 若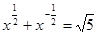 , 求
, 求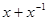 的值
的值

 ,则函数
,则函数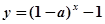 的图象必过点 ( )
的图象必过点 ( )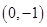
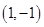
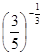 ,b=
,b=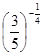 ,c=
,c=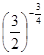 ,则a、b、c的大小关系是 ( )
,则a、b、c的大小关系是 ( )
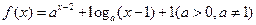 的图象必经过点_____▲_____
的图象必经过点_____▲_____ 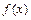 是定义在
是定义在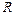 上的奇函数,当
上的奇函数,当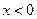 时,
时,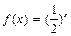 ,那么
,那么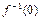 的值为( )
的值为( )