题目内容
7、n支球队要举行主客场双循环比赛(每两支球队比赛两场,各有一场主场比赛),每支球队在一周(从周日到周六的七天)内可以进行多场客场比赛.但如果某周内该球队有主场比赛,在这一周内不能安排该球队的客场比赛.如果4周内能够完成全部比赛,求n的最大值.
注:A、B两队在A方场地举行的比赛,称为A的主场比赛,B的客场比赛.
注:A、B两队在A方场地举行的比赛,称为A的主场比赛,B的客场比赛.
分析:由题意知,可以通过图表更清楚的表示比赛的安排,从图表可以验证出n=6,证明n不能是7,当n是7时,利用集合的观点解释,由于某周内该球队有主场比赛,在这一周内不能安排该球队的客场比赛,所以在球队比赛周次中中,没有一个集是另一个的子集.
解答: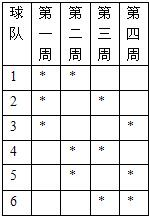 解:如图所示:表格中有“*”,
解:如图所示:表格中有“*”,
表示该球队在该周有主场比赛,不能出访.
容易验证,按照表中的安排,6支球队四周可以完成该项比赛.
下面证明7支球队不能在四周
完成该项比赛.设Si(i=1,2,3,4,5,6,7)表示
i号球队的主场比赛周次的集合.假设4周内
能完成该项比赛,则Si是{1,2,3,4}的非空真子集.
一方面由于某周内该球队有主场比赛,在这一周内不能安排该球队的客场比赛,所以Si(i=1,2,3,4,5,6,7)中,没有一个集是另一个的子集.
另一方面,设A=1,1,2,1,2,3,
B=2,2,3,2,3,4,
C=3,1,3,1,3,4
D=4,1,4,1,2,4,
E=2,4,
F=3,4由抽屉原理,一定存在i,j,i≠j,i,j∈{1,2,3,4,5},
Si,Sj属于同一集合A或B或C或D或E或F,必有Si⊆Sj或Sj⊆Si发生.
∴n的最大值是6.
 解:如图所示:表格中有“*”,
解:如图所示:表格中有“*”,表示该球队在该周有主场比赛,不能出访.
容易验证,按照表中的安排,6支球队四周可以完成该项比赛.
下面证明7支球队不能在四周
完成该项比赛.设Si(i=1,2,3,4,5,6,7)表示
i号球队的主场比赛周次的集合.假设4周内
能完成该项比赛,则Si是{1,2,3,4}的非空真子集.
一方面由于某周内该球队有主场比赛,在这一周内不能安排该球队的客场比赛,所以Si(i=1,2,3,4,5,6,7)中,没有一个集是另一个的子集.
另一方面,设A=1,1,2,1,2,3,
B=2,2,3,2,3,4,
C=3,1,3,1,3,4
D=4,1,4,1,2,4,
E=2,4,
F=3,4由抽屉原理,一定存在i,j,i≠j,i,j∈{1,2,3,4,5},
Si,Sj属于同一集合A或B或C或D或E或F,必有Si⊆Sj或Sj⊆Si发生.
∴n的最大值是6.
点评:这是一个比较难理解的问题,解题的关键是对于比赛的规则要理解清楚,这种题目若作为高考题是一个很大的突破,是一个考查理解和运算能力的问题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目