题目内容
设集合
是
的子集，如果点
满足：
，称
为集合的聚点.则下列集合中以
为聚点的有：
； ②
；③
；④
（ ）
| A．①④ | B．②③ | C．①② | D．①②④ |
A
解析试题分析：①中，集合中的元素是极限为1的数列，∴在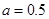
的时候，存在满足0＜|x－1|＜a的x，∴1是集合的聚点；②集合中的元素是极限为0的数列，最大值为2，即｜x－1｜≥1，对于某个a＞1，不存在0＜|x－1|
，∴1不是集合的聚点；③对于某个a＜1，比如a=0.5，此时对任意的x∈Z，都有|x﹣1|=0或者|x﹣1|≥1，也就是说不可能0＜|x﹣1|＜0.5，从而1不是整数集Z的聚点；④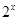
＞0，存在0＜|x－1|＜0.5的数x，从而1是整数集Z的聚点，故选A.
考点：集合，极限.
练习册系列答案
相关题目
已知集合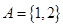
，
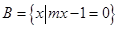，若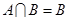
，则符合条件的实数
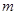的值组成的集合为（ ）
A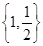． | B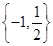． | C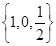． | D． |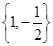
下列集合中,不同于另外三个集合的是（ ）
| A．{1} | B． |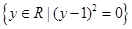
C． | D． |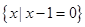
对于任意两个正整数m, n , 定义某种运算“※”如下：当m ,n都为正偶数或正奇数时,
※
=
当
中一个为正偶数,另一个为正奇数时,※=
.则在此定义下,集合
※
中的元素个数是( )
| A．10个 | B．15个 | C．16个 | D．18个 |
满足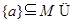
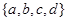的集合
共有（ ）
| A．6个 | B．5个 | C．8个 | D．7个 |
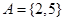设集合
，则集合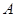
的子集个数是
| A．1 | B．2 | C．3 | D．4 |
若全集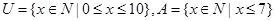
，则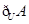
的元素个数（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
已知集合A＝{x∈R||x|≥2}，B＝{x∈R|x2－x－2＜0}，且R为实数集，则下列结论正确的是( )
| A．A∪B＝R | B．A∩B≠∅ |
| C．A⊆(∁RB) | D．A?(∁RB) |
若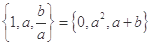
，则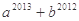
的值为( )
A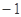． | B．1 | C．±1 | D．0 |