题目内容
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中
,其中 ,若
,若 ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为
A. | B. | C. | D. |
C
解析试题分析:(a,b)共有6×6=36种情况。猜数字游戏可能出现的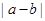 所有结果如下表所示:
所有结果如下表所示:
0 1 2 3 4 5
0 0 |-1| |-2| |-3| |-4| |-5|
1 1 0 |-1| |-2| |-3| |-4|
2 2 1 0 |-1| |-2| |-3|
3 3 2 1 0 |-1| |-2|
4 4 3 2 1 0 |-1|
5 5 4 3 2 1 0
其中,“心有灵犀”的结果总数为16,所以他们“心有灵犀”的概率为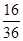 =
= 。故选C。
。故选C。
考点:本题主要考查古典概型概率的计算。
点评:基础题,也可利用“树图法”列出“心有灵犀”的情况,运用概率计算公式求解。

 一线名师提优试卷系列答案
一线名师提优试卷系列答案从集合 中随机取出一个数,设事件
中随机取出一个数,设事件 为“取出的数是偶数”, 事件
为“取出的数是偶数”, 事件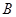 为“取出的数是奇数”,则事件
为“取出的数是奇数”,则事件 与
与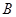
| A.是互斥且是对立事件 | B.是互斥且不对立事件 |
| C.不是互斥事件 | D.不是对立事件 |
从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是( )
| A.1 | B. | C. | D. |
从12件同类产品中,其中10件是正品,2件是次品,任意抽取3件的必然事件是
| A.3件都是正品 | B.至少1件是次品 |
| C.3件都是次品 | D.至少1件是正品 |
某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
| A.6 | B.8 | C.10 | D.12 |
已知随机变量x~ ,
, ,则
,则 ( )
( )
| A.0.16 | B.0.32 | C.0.68 | D. 0.84 |




 的面积大于
的面积大于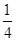 的概率是( )
的概率是( )





