题目内容
设P,Q是两个非空集合,定义集合间的一种运算“⊙”:P⊙Q={x|x∈P∪Q,且x∉P∩Q}.如果P={y|y= },Q={y|y=4x,x>0},则P⊙Q=( ).
},Q={y|y=4x,x>0},则P⊙Q=( ).
| A.[0,1]∪(4,+∞) | B.[0,1]∪(2,+∞) |
| C.[1,4] | D.(4,+∞) |
B
解析试题分析:本题首先求出集合P,Q,然后要正确理解新定义的运算“⊙”.通俗地讲P⊙Q是由集合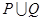 中把集合
中把集合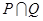 中含有的元素剔除,由剩下的元素所构成.
中含有的元素剔除,由剩下的元素所构成.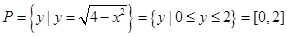 ,
,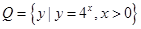
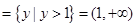 ,∴
,∴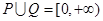 ,
,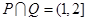 ,从而P⊙Q=[0,1]∪(2,+∞) .
,从而P⊙Q=[0,1]∪(2,+∞) .
考点:函数的值域与集合的运算.

练习册系列答案
相关题目
若集A={x|-1≤2x+1≤3},B={x| ≤0},则A∪B=( )
≤0},则A∪B=( )
| A.{x|-1≤x<2} | B.{x|-1≤x≤2} |
| C.{x|0≤x≤2} | D.{x|0≤x≤1} |
已知函数 的定义域为M,函数g(x)=
的定义域为M,函数g(x)= 的定义域为N,则
的定义域为N,则 ( )
( )
A. | B. | C. | D. |
已知全集为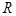 ,集合
,集合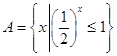 ,
,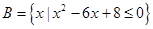 ,则
,则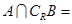 ( )
( )
A. | B.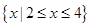 |
C.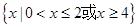 | D.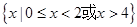 |
设 ,集合
,集合 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )
A. | B. |
C.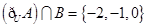 | D. |
已知集合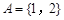 ,
,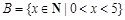 ,若
,若 ,则满足条件的集合
,则满足条件的集合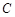 的个数为( )
的个数为( )
| A.4 | B.3 | C.2 | D.1 |
已知集合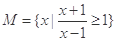 ,集合
,集合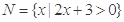 ,则
,则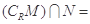 ( )
( )
A.(-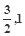 ) ) | B.(-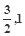 ] ] | C.[-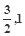 ) ) | D.[-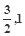 ] ] |
已知集合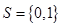 ,集合
,集合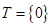 ,
,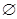 表示空集,那么
表示空集,那么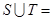 ( )
( )
A.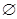 | B.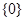 | C.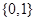 | D.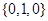 |
已知集合A={x|x2-2x>0},B={x|-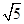 <x<
<x<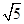 },则( )
},则( )
| A.A∩B=Æ | B.A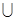 B=R B=R | C.B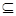 A A | D.A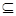 B B |