题目内容
在 中,S是它的面积,a,b是它的两条边的长度,S=
中,S是它的面积,a,b是它的两条边的长度,S= (a2+b2),求这个三角形的各内角。
(a2+b2),求这个三角形的各内角。
【答案】
∠A=∠B=45o,∠C0=90o.
【解析】
试题分析:∵S=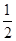 absinC,∴
absinC,∴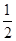 absinC=
absinC=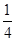 (a2+b2),
(a2+b2),
则a2+b2-2absinC=0.
(a+b)2+2ab(1-sinC)=0
∵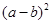 ≥0,2ab(1-sinC) ≥0
≥0,2ab(1-sinC) ≥0
∴ 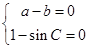

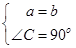
∴∠A=∠B=45o,∠C0=90o.
考点:本题主要考查正弦定理。
点评:三角形中边角互化问题,是常见的高考试题,本题利用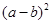 ≥0,2ab(1-sinC) ≥0得出等式,是解题的关键。
≥0,2ab(1-sinC) ≥0得出等式,是解题的关键。

练习册系列答案
相关题目
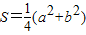 ,则△ABC的形状是( )
,则△ABC的形状是( )