题目内容
4、设圆C的方程x2+y2-2x-2y-2=0,直线L的方程(m+1)x-my-1=0,对任意实数m,圆C与直线L的位置关系是( )
分析:直线是直线系,过定点,判断定点的位置,从而求得结果.
解答:解:直线L的方程(m+1)x-my-1=0,化简为m(x-y)+(x-1)=0,过定点(1,1);
圆C的方程x2+y2-2x-2y-2=0,圆心坐标(1,1),显然圆C与直线L相交.
故选A.
圆C的方程x2+y2-2x-2y-2=0,圆心坐标(1,1),显然圆C与直线L相交.
故选A.
点评:本题考查直线与圆的位置关系,直线系方程,是基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
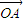 ,
,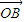 满足
满足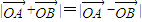 ,设圆C的方程为x2+y2-(x1+x2)x-(y1+y2)y=0.
,设圆C的方程为x2+y2-(x1+x2)x-(y1+y2)y=0.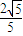 时,求p的值.
时,求p的值. ,
, 满足
满足 ,设圆C的方程为x2+y2-(x1+x2)x-(y1+y2)y=0.
,设圆C的方程为x2+y2-(x1+x2)x-(y1+y2)y=0. 时,求p的值.
时,求p的值. 时,求P的值.
时,求P的值.