题目内容
直角坐标系下,O为坐标原点,定点E(4,0),动点M(x,y)满足 •
• =x2.
=x2.(Ⅰ)求动点M(x,y)的轨迹C的方程;
(Ⅱ)过定点F(1,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值.
【答案】分析:(Ⅰ)根据动点M(x,y)满足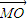 •
• =x2,建立方程,化简即可得到结论;
=x2,建立方程,化简即可得到结论;
(Ⅱ)设出直线l1,l2的方程与抛物线方程联立,利用韦达定理及抛物线的定义,求出|MN|、|RQ|,表示出面积,利用基本不等式,即可得到结论.
解答:解:(Ⅰ)由题意:动点M(x,y)满足 •
• =x2,
=x2,
∴(-x,-y)•(4-x,-y)=x2,即y2=4x为点M的轨迹方程.…(4分)
(Ⅱ)由题易知直线l1,l2的斜率都存在,且不为0,不妨设MN方程为y=k(x-1)
与y2=4x联立得:k2x2-(2k2+4)x+k2=0,
设M(x1,y1),N(x2,y2),
∴
由抛物线定义知:|MN|=|MF|+|NF|= …(7分)
…(7分)
同理RQ的方程为 ,求得|RQ|=4(k2+1).…(9分)
,求得|RQ|=4(k2+1).…(9分)
∴ . …(13分)
. …(13分)
当且仅当k2=1,k=±1时取“=”,
故四边形MRNQ的面积的最小值为32.…(15分)
点评:本题考查轨迹方程的求解,考查直线与抛物线的位置关系,考查韦达定理的运用,考查三角形面积的计算,考查基本不等式的运用,属于中档题.
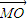 •
• =x2,建立方程,化简即可得到结论;
=x2,建立方程,化简即可得到结论;(Ⅱ)设出直线l1,l2的方程与抛物线方程联立,利用韦达定理及抛物线的定义,求出|MN|、|RQ|,表示出面积,利用基本不等式,即可得到结论.
解答:解:(Ⅰ)由题意:动点M(x,y)满足
 •
• =x2,
=x2,∴(-x,-y)•(4-x,-y)=x2,即y2=4x为点M的轨迹方程.…(4分)
(Ⅱ)由题易知直线l1,l2的斜率都存在,且不为0,不妨设MN方程为y=k(x-1)
与y2=4x联立得:k2x2-(2k2+4)x+k2=0,
设M(x1,y1),N(x2,y2),
∴

由抛物线定义知:|MN|=|MF|+|NF|=
 …(7分)
…(7分)同理RQ的方程为
 ,求得|RQ|=4(k2+1).…(9分)
,求得|RQ|=4(k2+1).…(9分)∴
 . …(13分)
. …(13分)当且仅当k2=1,k=±1时取“=”,
故四边形MRNQ的面积的最小值为32.…(15分)
点评:本题考查轨迹方程的求解,考查直线与抛物线的位置关系,考查韦达定理的运用,考查三角形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目