题目内容
若椭圆E1: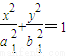 和椭圆E2:
和椭圆E2: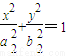 满足
满足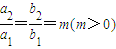 ,则称这两个椭圆相似,m是相似比.
,则称这两个椭圆相似,m是相似比.(Ⅰ)求过(
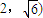 且与椭圆
且与椭圆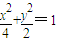 相似的椭圆的方程;
相似的椭圆的方程;(Ⅱ)设过原点的一条射线l分别于(I)中的两椭圆交于A、B两点(点A在线段OB上).求|OA|•|OB|的最大值和最小值.
【答案】分析:(1)直接根据定义得到有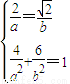 解得a,b.即可得到与椭圆
解得a,b.即可得到与椭圆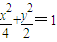 相似的椭圆方程;
相似的椭圆方程;
(2)先求出当射线l的斜率不存在时求出结论;再对当射线l的斜率存在时,设其方程y=kx,联立直线与两个椭圆方程分别求出线段的长度,再结合函数的单调性即可求出|OA|•|OB|的最大值和最小值.
解答:解:(Ⅰ)设与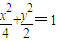 相似的椭圆的方程
相似的椭圆的方程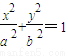 ,
,
有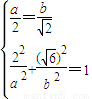 ⇒
⇒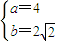 .
.
所求方程是 .…(6分)
.…(6分)
(Ⅱ)当射线l的斜率不存在时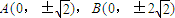 .
.
设点P坐标P(0,y),则y2=4,y=±2.即P(0,±2).…(8分)
当射线l的斜率存在时,设其方程y=kx,P(x,y)
由A(x1,y1),B(x2,y2)则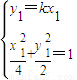 得
得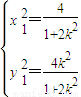 ,
,
∴ ,
,
同理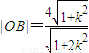 .…(10分)
.…(10分)
当l的斜率不存在时,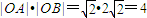 ,
,
当l的斜率存在时,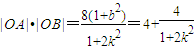 ,
,
∴4<|OA|•|OB|≤8,
综上,|OA|•|OB|的最大值是8,最小值是4.…(12分)
点评:本题综合考查直线和椭圆的位置关系,难度较大,解题时要仔细审题,注意公式的灵活运用.
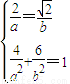 解得a,b.即可得到与椭圆
解得a,b.即可得到与椭圆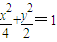 相似的椭圆方程;
相似的椭圆方程;(2)先求出当射线l的斜率不存在时求出结论;再对当射线l的斜率存在时,设其方程y=kx,联立直线与两个椭圆方程分别求出线段的长度,再结合函数的单调性即可求出|OA|•|OB|的最大值和最小值.
解答:解:(Ⅰ)设与
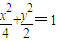 相似的椭圆的方程
相似的椭圆的方程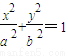 ,
,有
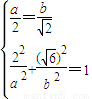 ⇒
⇒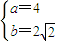 .
.所求方程是
 .…(6分)
.…(6分)(Ⅱ)当射线l的斜率不存在时
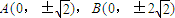 .
.设点P坐标P(0,y),则y2=4,y=±2.即P(0,±2).…(8分)
当射线l的斜率存在时,设其方程y=kx,P(x,y)
由A(x1,y1),B(x2,y2)则
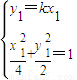 得
得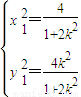 ,
,∴
 ,
,同理
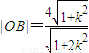 .…(10分)
.…(10分)当l的斜率不存在时,
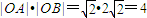 ,
,当l的斜率存在时,
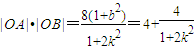 ,
,∴4<|OA|•|OB|≤8,
综上,|OA|•|OB|的最大值是8,最小值是4.…(12分)
点评:本题综合考查直线和椭圆的位置关系,难度较大,解题时要仔细审题,注意公式的灵活运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,已知椭圆E1方程为
如图,已知椭圆E1方程为 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.