题目内容
已知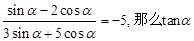 的值为( )
的值为( )
| A.-2 | B.2 | C. | D.- |
D
解析试题分析: 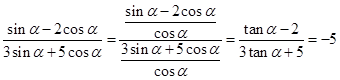 ,解得
,解得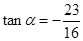 。故D正确。
。故D正确。
考点:同角三角函数关系式。

练习册系列答案
相关题目
方程|x|=cosx在(-∞,+∞)内( )
| A.没有根 | B.有且仅有一个根 |
| C.有且仅有两个根 | D.有无穷多个根 |
已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为0.两个对称轴间最短距离为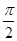 ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式为( )
是其图象的一条对称轴,则符合条件的解析式为( )
A.y=4sin  | B.y=-2sin  +2 +2 |
C.y=-2sin  | D.y=2sin  +2 +2 |
已知sin 2α= ,则cos2
,则cos2 =( )
=( )
A.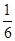 | B. | C. | D. |
设函数y=Asin(ωx+φ)(A>0,ω>0)在x= 时,取最大值A,在x=
时,取最大值A,在x= 时,取最小值-A,则当x=π时,函数y的值( )
时,取最小值-A,则当x=π时,函数y的值( )
| A.仅与ω有关 | B.仅与φ有关 |
| C.等于零 | D.与φ,ω均有关 |
函数y=- cos2x+
cos2x+ 的递增区间是( )
的递增区间是( )
A.(kπ,kπ+ )(k∈Z) )(k∈Z) |
B.(kπ+ ,kπ+π)(k∈Z) ,kπ+π)(k∈Z) |
| C.(2kπ,2kπ+π)(k∈Z) |
| D.(2kπ+π,2kπ+2π)(k∈Z) |
将函数y=sin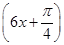 的图像上各点向右平移
的图像上各点向右平移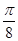 个单位,则得到新函数的解析式为( )
个单位,则得到新函数的解析式为( )
A.y=sin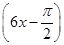 | B.y=sin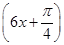 | C.y=sin | D.y=sin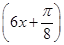 |
 的部分图象如图示,则将
的部分图象如图示,则将 的图象向右平移
的图象向右平移 个单位后,得到的图象解析式为( )
个单位后,得到的图象解析式为( )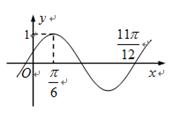




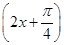 的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的
的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的 倍,所得图象关于直线x=
倍,所得图象关于直线x=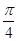 对称.则φ的最小正值为( )
对称.则φ的最小正值为( )