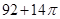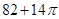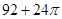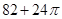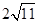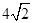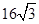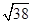题目内容
已知三棱柱
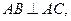

A.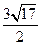 |
B. |
C. |
D.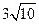 |
C
解析法一:由球心作面ABC的垂线,则垂足为斜边BC中点M.计算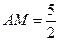 ,由垂径定理,
,由垂径定理,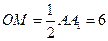 以半径R=
以半径R=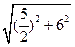 =
=
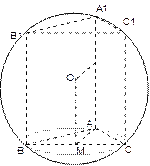
法二:由题设知题中三棱柱可视为长方体的一部分,且长方体同一顶点的三条棱分别为3,4,12,三棱柱的外接球即为长方体之外接球,所以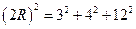
∴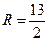

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
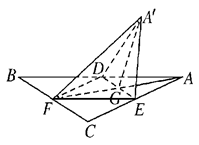
如图,等边三角形 的中线
的中线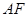 与中位线
与中位线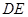 相交于
相交于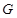 ,已知
,已知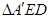 是△
是△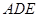 绕
绕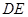 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( )
A.动点 在平面 在平面 上的射影在线段 上的射影在线段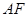 上 上 |
B.恒有平面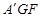 ⊥平面 ⊥平面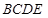 |
C.三棱锥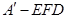 的体积有最大值 的体积有最大值 |
D.异面直线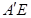 与 与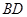 不可能垂直 不可能垂直 |
正四面体的外接球和内切球的半径的关系是( )
A. |
B.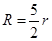 |
C.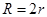 |
D.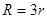 |
一个正三棱柱的三视图如图所示,这个三棱柱的侧(左)视图的面积为 ,则这个三棱柱的体积为 ( )
,则这个三棱柱的体积为 ( )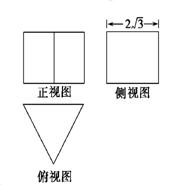
| A.12 | B.16 | C.8 | D.12 |
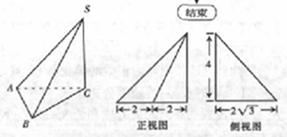
某几何体的三视图如图所示,该几何体的体积是( ) 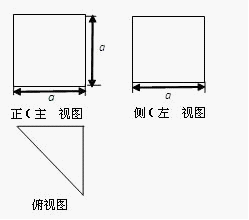
A. |
B. |
C.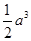 |
D.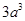 |
如图,正方体的底面与正四面体的底面在同一平面 上,且
上,且 ,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为
,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为 ,那么
,那么 ( )
( )
| A.8 |
| B.9 |
| C.10 |
| D.11 |
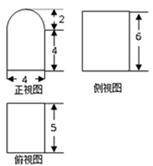
某空间几何体的三视图如图所示,则该几何体的表面积为( )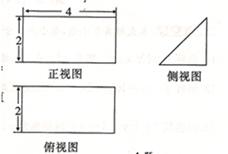
A.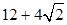 | B. | C. | D.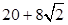 |