题目内容
已知平面a ∥平面b ，AB、CD是夹在两平行平面问的两条线段，A、C在a 内．B、C在b 内，点E、F分别在AB、CD上．且AE∶EB=CF∶FD=m∶n．求证：EF∥a ．
答案：略
解析：
解析：
|
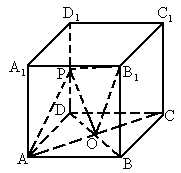
证明 分 AB，CD是异面、共面两种情况讨论．(1) 当AB、CD共面时，如图．
∵a ∥b ，∴ AC∥BD，连E、F．∵ AE∶EB=CF∶FD，∴ EF∥AC∥BD且EF
a
，ACÌ
a
，
∴ EF∥a ，(2) 当AB，CD异面时，如图，过点A作AH∥CD交b 于点H．
在 H上取点G，使AG∶GH=m∶n，连EF，由(1) 证明可得GF∥HD，又 AG∶GH=AE∶EB，得EG∥BH，∴平面 EFG∥平面b ∥平面a ，又 EFÌ 面EFG，∴EF∥a ． |
练习册系列答案
阅读快车系列答案
相关题目
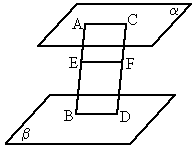
，则在b
内与直线a相距为2d的直线有
，则a
与b
的距离等于a
与b
的距离
且a∥b，则a与b的距离等于a
与b
的距离
且a、b异面，则a与b的距离等于a
与b
的距离