题目内容
下面命题中,正确命题的个数为( )①若
 1、
1、 2分别是平面α、β的法向量,则
2分别是平面α、β的法向量,则 1∥
1∥ 2?α∥β;
2?α∥β;②若
 1、
1、 2分别是平面α、β的法向量,则α⊥β?
2分别是平面α、β的法向量,则α⊥β? 1•
1• 2=0;
2=0;③若
 是平面α的法向量,
是平面α的法向量, 、
、 是α内两不共线向量
是α内两不共线向量 =λ
=λ +μ
+μ ,(λ,μ∈R)则
,(λ,μ∈R)则 •
• =0;
=0;④若两个平面的法向量不垂直,则这两个平面一定不垂直.
A.1个
B.2个
C.3个
D.4个
【答案】分析:①由面面平行得法向量共线,反之两平面平行或重合,由此即作出可判断;②由面面垂直的定义及性质即可判断;③由线面垂直的性质及向量共面定理判断④由面面垂直的定义判断.
解答:解:①中由α∥β可得 1∥
1∥ 2,由
2,由 1∥
1∥ 2可得,平面α与β可能平行,也可能重合,所以①不正确,
2可得,平面α与β可能平行,也可能重合,所以①不正确,
②α⊥β,则二面角的平面角成90°,由圆的内接四边形对顶角互补知法向量垂直,反之当法向量垂直,则二面角成90°,由圆内接四边形对顶角互补,知两平面垂直.故②正确;
③由a=λb+μc,知三向量共面,则a在平面α内或与平面α平行,所以平面的法向量与直线a垂直,故③正确.
④若两个平面的法向量不垂直,则所成角不是90°,则由圆内接四边形对顶角互补知两平面所成的角不是90°,故④正确.
故选C.
点评:本题主要考查用向量法来解决面面平行,面面垂直等问题,原理应从几何法角度去理解,才能灵活准确地应用.
解答:解:①中由α∥β可得
 1∥
1∥ 2,由
2,由 1∥
1∥ 2可得,平面α与β可能平行,也可能重合,所以①不正确,
2可得,平面α与β可能平行,也可能重合,所以①不正确,②α⊥β,则二面角的平面角成90°,由圆的内接四边形对顶角互补知法向量垂直,反之当法向量垂直,则二面角成90°,由圆内接四边形对顶角互补,知两平面垂直.故②正确;
③由a=λb+μc,知三向量共面,则a在平面α内或与平面α平行,所以平面的法向量与直线a垂直,故③正确.
④若两个平面的法向量不垂直,则所成角不是90°,则由圆内接四边形对顶角互补知两平面所成的角不是90°,故④正确.
故选C.
点评:本题主要考查用向量法来解决面面平行,面面垂直等问题,原理应从几何法角度去理解,才能灵活准确地应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
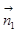 、
、 分别是平面
分别是平面 的法向量,则
的法向量,则 ;
; ;
; 是平面α的法向量,
是平面α的法向量, 是
是 内两不共线向量,
内两不共线向量,
 ;
; ,对于数列
,对于数列 ,令
,令 为
为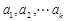 中的最大值,称数列
中的最大值,称数列 为
为 的
的 的递进上限数列为2,2,3,7,7.则下面命题中
的递进上限数列为2,2,3,7,7.则下面命题中 ,则数列
,则数列