题目内容
为了保障生命安全,国家有关部门发布的《车辆驾驶人员血液呼气酒精含量阀值与检验》中规定:车辆驾驶人员血液酒精含量(单位:mg/l00m1)大于或者等于20,且小于80的为“饮酒驾车”,大于或者等于80的为“醉酒驾车”.某城市3月份的交通执法部门对200名车辆驾驶人员的血液酒精含量(单位:mg/l00ml )进行测试,并根据测试的数据作了如下统计:
| 组号 | 分组 | 频数 | 频率 |
| 1 | [0,20) | 162 | 0.81 |
| 2 | [20,40) | 18 | 0.09 |
| 3 | [40,60) | 10 | y |
| 4 | [60,80) | 6 | 0.03 |
| 5 | [80,100) | x | 0.02 |
(2)试估计该城市3月份“饮酒驾车”发生的概率;
(3)若在第3,4,5组用分层抽样的方法随机抽取10人做回访调查,并在这10人中任选2人做回访,求这两人中恰有1人是醉酒驾车的概率.
解:(1)由题意可得 x=200×0.02=4,y= =0.05.
=0.05.
(2)根据“饮酒驾车”的规定可得“饮酒驾车”发生的概率为0.09+0.05+0.03=0.17.
(3)在第3,4,5组用分层抽样的方法随机抽取的人数分别为10× =5,
=5,
10× =3,10×
=3,10× =2.
=2.
其中只有第5组中的2个人醉酒驾驶,故这两人中恰有1人是醉酒驾车的概率为 =
=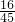 .
.
分析:(1)用样本容量乘以该层的频率,即得该层的频数;该层的频率等于该层的频数除以样本容量.
(2)饮酒驾车”发生的概率为第二、三、四组的频率之和.
(3)先求出在第3,4,5组用分层抽样的方法随机抽取的人数,只有第5组中的2个人醉酒驾驶,故这两人中恰有1人是醉酒驾车的概率为 ,运算求得结果.
,运算求得结果.
点评:本题主要考查等可能事件的概率,频率分布表的应用,属于基础题.
 =0.05.
=0.05.(2)根据“饮酒驾车”的规定可得“饮酒驾车”发生的概率为0.09+0.05+0.03=0.17.
(3)在第3,4,5组用分层抽样的方法随机抽取的人数分别为10×
 =5,
=5,10×
 =3,10×
=3,10× =2.
=2.其中只有第5组中的2个人醉酒驾驶,故这两人中恰有1人是醉酒驾车的概率为
 =
=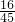 .
.分析:(1)用样本容量乘以该层的频率,即得该层的频数;该层的频率等于该层的频数除以样本容量.
(2)饮酒驾车”发生的概率为第二、三、四组的频率之和.
(3)先求出在第3,4,5组用分层抽样的方法随机抽取的人数,只有第5组中的2个人醉酒驾驶,故这两人中恰有1人是醉酒驾车的概率为
 ,运算求得结果.
,运算求得结果.点评:本题主要考查等可能事件的概率,频率分布表的应用,属于基础题.

练习册系列答案
相关题目
为了保障生命安全,国家有关部门发布的《车辆驾驶人员血液呼气酒精含量阀值与检验》中规定:车辆驾驶人员血液酒精含量(单位:mg/l00m1)大于或者等于20,且小于80的为“饮酒驾车”,大于或者等于80的为“醉酒驾车”.某城市3月份的交通执法部门对200名车辆驾驶人员的血液酒精含量(单位:mg/l00ml )进行测试,并根据测试的数据作了如下统计:
(1)求x,y的值(要求列出算式及计算出结果);
(2)试估计该城市3月份“饮酒驾车”发生的概率;
(3)若在第3,4,5组用分层抽样的方法随机抽取10人做回访调查,并在这10人中任选2人做回访,求这两人中恰有1人是醉酒驾车的概率.
| 组号 | 分组 | 频数 | 频率 |
| 1 | [0,20) | 162 | 0.81 |
| 2 | [20,40) | 18 | 0.09 |
| 3 | [40,60) | 10 | y |
| 4 | [60,80) | 6 | 0.03 |
| 5 | [80,100) | x | 0.02 |
(2)试估计该城市3月份“饮酒驾车”发生的概率;
(3)若在第3,4,5组用分层抽样的方法随机抽取10人做回访调查,并在这10人中任选2人做回访,求这两人中恰有1人是醉酒驾车的概率.