题目内容
已知向量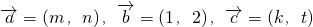 ,且
,且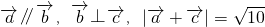 ,则mt的取值范围是
,则mt的取值范围是
- A.(-∞,1]
- B.(0,1]
- C.[-1,1]
- D.(-1,1)
A
分析:利用向量共线的充要条件和垂直的充要条件得到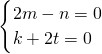 ,再结合向量的模的公式得出m2+t2=2,最后利用基本不等式求出mt的取值范围即可.
,再结合向量的模的公式得出m2+t2=2,最后利用基本不等式求出mt的取值范围即可.
解答:∵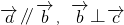 ,
,
∴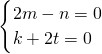 ,
,
∵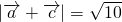 ,
,
∴(m+k)2+(n+t)2=10,
从而有:(m-2t)2+(2m+t)2=10,化简得:m2+t2=2,
由基本不等式得:mt≤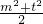 =1,当且仅当m=t时取等号,
=1,当且仅当m=t时取等号,
则mt的取值范围是(-∞,1].
故选A.
点评:本题考查向量垂直的充要条件,考查向量共线的充要条件,考查平面向量数量积的坐标表示等,属于基础题.
分析:利用向量共线的充要条件和垂直的充要条件得到
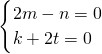 ,再结合向量的模的公式得出m2+t2=2,最后利用基本不等式求出mt的取值范围即可.
,再结合向量的模的公式得出m2+t2=2,最后利用基本不等式求出mt的取值范围即可.解答:∵
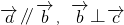 ,
,∴
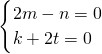 ,
,∵
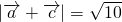 ,
,∴(m+k)2+(n+t)2=10,
从而有:(m-2t)2+(2m+t)2=10,化简得:m2+t2=2,
由基本不等式得:mt≤
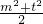 =1,当且仅当m=t时取等号,
=1,当且仅当m=t时取等号,则mt的取值范围是(-∞,1].
故选A.
点评:本题考查向量垂直的充要条件,考查向量共线的充要条件,考查平面向量数量积的坐标表示等,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
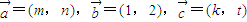 ,且
,且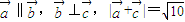 ,则mt的取值范围是( )
,则mt的取值范围是( )