题目内容
若函数y=x2+(2a-1)x+1在区间(-∞,2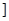 上是减函数,则实数a的取值范围是( )
上是减函数,则实数a的取值范围是( )
A  -
- ,+∞) B (-∞,-
,+∞) B (-∞,-
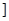 C
C 
 ,+∞) D (-∞,
,+∞) D (-∞,
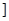
B
解析

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
函数 的定义域为( )
的定义域为( )
A. | B. | C.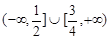 | D. |
设函数 的定义域为
的定义域为 ,若对于任意
,若对于任意 且
且 ,恒有
,恒有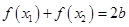 ,则称点
,则称点 为函数
为函数 图象的对称中心.研究并利用函数
图象的对称中心.研究并利用函数 的对称中心,可得
的对称中心,可得 ( )
( )
| A.4023 | B.-4023 | C.8046 | D.-8046 |
设函数 ,则
,则 的值为( )
的值为( )
A. | B. |
C. 中较小的数 中较小的数 | D. 中较大的数 中较大的数 |
若 ,则函数
,则函数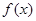 = ( )
= ( )
A.f(x)=  | B.f(x)=  | C.f(x)=  | D.f(x)=  |
如果函数 对于任意实数
对于任意实数 ,存在常数
,存在常数 ,使该不等式
,使该不等式 恒成立,就称函数
恒成立,就称函数 为有界泛涵,下面有4个函数:①
为有界泛涵,下面有4个函数:① ②
②
③ ④
④ ,其中有两个属于有界泛涵,它们是( )
,其中有两个属于有界泛涵,它们是( )
| A.①② | B.②④ | C.①③ | D.③④ |
设函数f(x)是定义在R上的奇函数,且f(-3)=-2,则f(3)+f(0)=( )
| A.3 | B.-3 | C.2 | D.7 |
若奇函数 在
在 上是增函数,且最小值是1,则它在
上是增函数,且最小值是1,则它在 上是( )
上是( )
| A.增函数且最小值是-1 | B.增函数且最大值是-1 |
| C.减函数且最大值是-1 | D.减函数且最小值是-1 |
 表示一个圆
表示一个圆 则( )
则( )






