题目内容
已知函数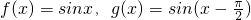 ,下列结论正确的是
,下列结论正确的是
- A.函数g(x)是奇函数
- B.点
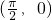 是函数f(x)的对称中心
是函数f(x)的对称中心 - C.函数f(x)•g(x)的最小正周期是π
- D.函数g(x)向右平移
 个单位可得到函数f(x)
个单位可得到函数f(x)
C
分析:根据函数g(x)=-cosx是偶函数,故A不正确.x= 时,y=1,可得点
时,y=1,可得点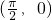 不是函数f(x)的对称中心.由于f(x)•g(x)=-
不是函数f(x)的对称中心.由于f(x)•g(x)=- sin2x,最小正周期等于 π,故C正确.
sin2x,最小正周期等于 π,故C正确.
函数g(x)向右平移 个单位可得到函数y=-sinx 的图象,故D不正确,综合可得结论.
个单位可得到函数y=-sinx 的图象,故D不正确,综合可得结论.
解答:∵已知函数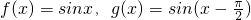 =-cosx,∴函数g(x)是偶函数,故A不正确.
=-cosx,∴函数g(x)是偶函数,故A不正确.
由于f(x)=sinx 是奇函数,x= 时,y=1,故点
时,y=1,故点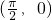 不是函数f(x)的对称中心,故B不正确.
不是函数f(x)的对称中心,故B不正确.
由于函数f(x)•g(x)=-sinxcosx=- sin2x,故它的最小正周期等于
sin2x,故它的最小正周期等于  =π,故C正确.
=π,故C正确.
函数g(x)向右平移 个单位可得到函数y=-cos(x-
个单位可得到函数y=-cos(x- )=-cos(
)=-cos( -x)=-sinx 的图象,故D不正确.
-x)=-sinx 的图象,故D不正确.
故选C.
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的对称性、周期性以及求法,y=Asin(ωx+∅)的图象变换规律,属于中档题.
分析:根据函数g(x)=-cosx是偶函数,故A不正确.x=
 时,y=1,可得点
时,y=1,可得点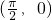 不是函数f(x)的对称中心.由于f(x)•g(x)=-
不是函数f(x)的对称中心.由于f(x)•g(x)=- sin2x,最小正周期等于 π,故C正确.
sin2x,最小正周期等于 π,故C正确.函数g(x)向右平移
 个单位可得到函数y=-sinx 的图象,故D不正确,综合可得结论.
个单位可得到函数y=-sinx 的图象,故D不正确,综合可得结论.解答:∵已知函数
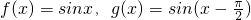 =-cosx,∴函数g(x)是偶函数,故A不正确.
=-cosx,∴函数g(x)是偶函数,故A不正确.由于f(x)=sinx 是奇函数,x=
 时,y=1,故点
时,y=1,故点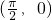 不是函数f(x)的对称中心,故B不正确.
不是函数f(x)的对称中心,故B不正确.由于函数f(x)•g(x)=-sinxcosx=-
 sin2x,故它的最小正周期等于
sin2x,故它的最小正周期等于  =π,故C正确.
=π,故C正确.函数g(x)向右平移
 个单位可得到函数y=-cos(x-
个单位可得到函数y=-cos(x- )=-cos(
)=-cos( -x)=-sinx 的图象,故D不正确.
-x)=-sinx 的图象,故D不正确.故选C.
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的对称性、周期性以及求法,y=Asin(ωx+∅)的图象变换规律,属于中档题.

练习册系列答案
相关题目
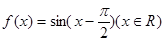 ,下列结论错误的是( )
,下列结论错误的是( )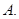 函数
函数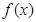 的最小正周期为
的最小正周期为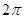
 函数
函数 函数
函数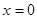 对称
对称  函数
函数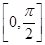 上是增函数
上是增函数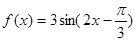 ,下列结论中正确的是(
)
,下列结论中正确的是(
)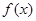 的最小正周期为
的最小正周期为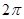 ; B.函数
; B.函数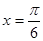 对称;
对称;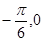 )对称;
)对称; 内是增函数.
内是增函数.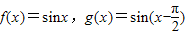 ,下列结论正确的是( )
,下列结论正确的是( )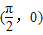 是函数f(x)的对称中心
是函数f(x)的对称中心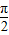 个单位可得到函数f(x)
个单位可得到函数f(x)