题目内容
下列对应中是集合A到B上的一一映射的是( )
分析:根据映射、一一映射的定义,判断各个选项中的对应是否是映射、是否是一一映射,从而得出结论.
解答:解:由于A中的元素0,按照映射f:x→y=
,在B中无像,故不是映射,故排除A.
若A=R,B=R,按照映射 f:x→y=-
,A中每个元素在B中都有唯一的一个元素与之对应,
反之,B中每个元素y在A中都有唯一的一个元素x与之对应,故f:x→y=-
是集合A到B上的一一映射.
若A=R,B=R,按照映射f:y=x6,A种每个元素在B中都有唯一的一个元素与之对应,
但B中有的元素(如-2等)在A中没有素与之对应,故不是A到B上的一一映射.
若A={x|x≥0},B={y|y>0},则对应f:x→y=|x|不是映射,因为A中元素0在B中没有元素与之对应,故不是映射.
故选B.
| 1 |
| x |
若A=R,B=R,按照映射 f:x→y=-
| 3 | x |
反之,B中每个元素y在A中都有唯一的一个元素x与之对应,故f:x→y=-
| 3 | x |
若A=R,B=R,按照映射f:y=x6,A种每个元素在B中都有唯一的一个元素与之对应,
但B中有的元素(如-2等)在A中没有素与之对应,故不是A到B上的一一映射.
若A={x|x≥0},B={y|y>0},则对应f:x→y=|x|不是映射,因为A中元素0在B中没有元素与之对应,故不是映射.
故选B.
点评:本题主要考查映射、一一映射的定义,属于基础题.

练习册系列答案
相关题目

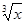
 ,B={y|0<y<1
,B={y|0<y<1