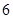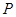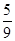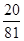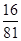题目内容
我校社团联即将举行一届象棋比赛,规则如下:两名选手比赛时,每局胜者得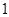 分,负者得
分,负者得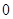 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响.
(Ⅰ)求比赛进行 局结束,且乙比甲多得
局结束,且乙比甲多得 分的概率;
分的概率;
(Ⅱ)设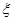 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量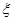 的分布列和数学期望.
的分布列和数学期望.
【答案】
(Ⅰ)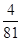 ;(Ⅱ)随机变量
;(Ⅱ)随机变量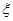 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
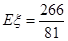
【解析】
试题分析:(Ⅰ)这是一个独立重复试验,比赛进行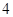 局结束,且乙比甲多得
局结束,且乙比甲多得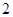 分,只能是前两局乙胜一局,3,4局乙连胜,根据独立重复试验从而求出,值得注意的是,做这一类题,一定分析清楚,否则容易出错;(Ⅱ)设
分,只能是前两局乙胜一局,3,4局乙连胜,根据独立重复试验从而求出,值得注意的是,做这一类题,一定分析清楚,否则容易出错;(Ⅱ)设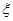 表示比赛停止时已比赛的局数,
表示比赛停止时已比赛的局数,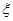 只能取值
只能取值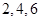 ,不能为3,5,分别求出
,不能为3,5,分别求出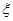 的取值为
的取值为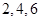 的概率,列分布列,从而求出数学期望,易错点为
的概率,列分布列,从而求出数学期望,易错点为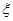 的取值不正确,导致分布列错误。
的取值不正确,导致分布列错误。
试题解析:(Ⅰ)由题意知,乙每局获胜的概率皆为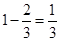 .比赛进行
.比赛进行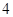 局结束,且乙比甲多得
局结束,且乙比甲多得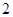 分即头两局乙胜一局,3,4局连胜,则
分即头两局乙胜一局,3,4局连胜,则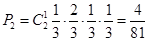 .
.
(Ⅱ)由题意知,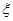 的取值为
的取值为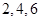 .则
.则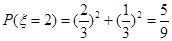
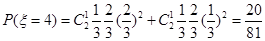 ,
,
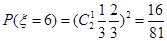 ,所以随机变量
,所以随机变量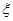 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
则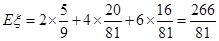
考点:本题考查独立重复事件的概率计算、离散型随机变量的分布列、期望,考查学生的逻辑推理能力以及基本运算能力.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目