题目内容
下列函数既是偶函数,在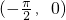 上又是减函数的是
上又是减函数的是
- A.y=sin2x
- B.y=cos2x
- C.y=e|x|
- D.
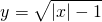
C
分析:由于y=sin2x是奇函数,故排除A.由于y=cos2x在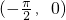 是增函数,故排除B.利用复合函数的单调性规律可得偶函数y=e|x| 在
是增函数,故排除B.利用复合函数的单调性规律可得偶函数y=e|x| 在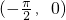 上是减函数,故满足条件.
上是减函数,故满足条件.
由于y=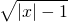 是偶函数,但在(-1,0)无意义,故不满足条件,故排除D.
是偶函数,但在(-1,0)无意义,故不满足条件,故排除D.
解答:由于y=sin2x是奇函数,不满足条件,故排除.
由于y=cos2x是偶函数,但此函数在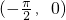 是增函数,故不满足条件,故排除.
是增函数,故不满足条件,故排除.
由于函数 y=e|x| 是偶函数,且|x|在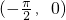 上是减函数,故y=e|x| 在
上是减函数,故y=e|x| 在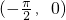 上是减函数,故满足条件.
上是减函数,故满足条件.
由于y=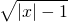 是偶函数,但在(-1,0)无意义,故不满足条件,故排除.
是偶函数,但在(-1,0)无意义,故不满足条件,故排除.
故选C.
点评:本题主要考查函数的奇偶性的判断,函数的单调性的判断和证明,属于中档题.
分析:由于y=sin2x是奇函数,故排除A.由于y=cos2x在
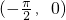 是增函数,故排除B.利用复合函数的单调性规律可得偶函数y=e|x| 在
是增函数,故排除B.利用复合函数的单调性规律可得偶函数y=e|x| 在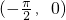 上是减函数,故满足条件.
上是减函数,故满足条件.由于y=
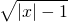 是偶函数,但在(-1,0)无意义,故不满足条件,故排除D.
是偶函数,但在(-1,0)无意义,故不满足条件,故排除D.解答:由于y=sin2x是奇函数,不满足条件,故排除.
由于y=cos2x是偶函数,但此函数在
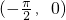 是增函数,故不满足条件,故排除.
是增函数,故不满足条件,故排除.由于函数 y=e|x| 是偶函数,且|x|在
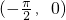 上是减函数,故y=e|x| 在
上是减函数,故y=e|x| 在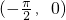 上是减函数,故满足条件.
上是减函数,故满足条件.由于y=
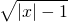 是偶函数,但在(-1,0)无意义,故不满足条件,故排除.
是偶函数,但在(-1,0)无意义,故不满足条件,故排除.故选C.
点评:本题主要考查函数的奇偶性的判断,函数的单调性的判断和证明,属于中档题.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 上又是减函数的是( )
上又是减函数的是( )
