题目内容
设a、b、c是互不相等的非零实数,试证:三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0中至少有一个方程有两个相异实根.
解:假设这三个方程均没有两个相异实根,也就是说这三个方程或者没有实根,或者有两个相等实根.
∴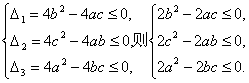
三式相加,得(a-b)2+(a-c)2+(b-c)2≤0.
则a=b=c,这与题设a、b、c各不相同矛盾,故假设不能成立,所以要证结论成立.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
题目内容
设a、b、c是互不相等的非零实数,试证:三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0中至少有一个方程有两个相异实根.
解:假设这三个方程均没有两个相异实根,也就是说这三个方程或者没有实根,或者有两个相等实根.
∴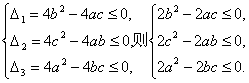
三式相加,得(a-b)2+(a-c)2+(b-c)2≤0.
则a=b=c,这与题设a、b、c各不相同矛盾,故假设不能成立,所以要证结论成立.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案