Question

（2013•合肥二模）点（x，y）满足

x+y-1≥0 x-y+1≥0 x≤a

，若目标函数z=x-2y的最大值为1，则实数a的值是（　　）

A．1

B．-1

C．-3

D．3

Answer 1

分析：先画出可行域，结合图形分析出目标函数z=x-2y取得最大值时对应点的坐标，把其代入目标函数再结合目标函数z=x-2y的最大值为1，即可求出实数a的值．

解答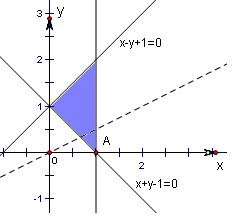：解：实数x，y满足不等式组

x+y-1≥0 x-y+1≥0 x≤a

，如图，
由图可知，当x=a，y=1-a时，
目标函数z=x-2y取得最大值，
即1=a-2×（1-a），解得：a=1
故选A．

点评：本题主要考查简单线性规划的应用以及数形结合思想的应用．在求目标函数的最值时，一般是在可行域的特殊点处，所以一般在解选择和填空题时，常用特殊点代入法．